2023.10.22 2024.05.26

笑わない数学（シーズン２）「1＋1＝2」が正しい理由のまとめ

kikorikori

記事内に商品プロモーションを含む場合があります

今回のテーマは「1＋1＝2」が正しい理由

これは数学基礎論に位置付けられている

証明するためには
「数」とは何か？
＋などの「演算」とは何か？
を定義する必要がある
（物質・物体などの「数え方」に関しては認識論の話になってきて脱線してしまうので割愛する）

ジュゼッペ・ペアノ（1858−1932、イタリア）
先の疑問を解決するために数学界に投げかけた
まずは「数」の集まりは存在するのか？
これは集合論の話であり、存在すると定義する

次に「0」は数であるか？
これも同様に「０」は数であると定義とする

「a」が数ならば「aの次」も数の一つであるか？
これも同様である

数論・代数学はこれらの定義がなくては成り立たない
まず最初の数というものに「1」という名前をつけよう
そして「1」の次は「2」と名付けよう
「2」の次は「3」と名付けよう
・
・
・
といったように具体的な「数」を定義した
（勿論、「0」の次は「1」であるも定義している）

次は「演算」について

足し算とは一体何なのか？

aとbが「数」のとき、a＋ bも「数」である
これも先ほどの定義から成り立つ

ということは
a＋0＝a・・・①式
であることが理解できると思う（両辺ともに「数」である）

a＋（bの次）＝（a＋ b）の次・・・②式
数が連続した数直線を考える

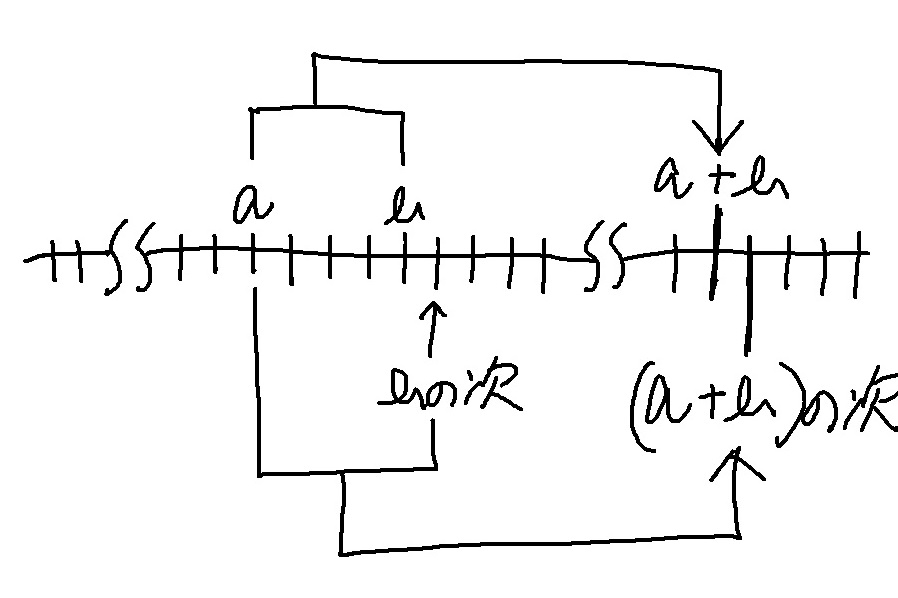
すると上式も成り立つのが分かる（両辺ともに「数」である）

この①式と②式が基本となる式

（ここで足し算の詳しい「性質」については、
　abc予想によって掛け算と違い「特異な演算」であることが投げかけられている）

さて、
ここからが本題の「1＋1＝2」であることの証明をしよう

1は「0の次」と定義しているので、
1 ＋ 1 ＝ 0の次＋ 0の次・・・③式
と書き表せる

先ほどの②式に「a ＝ 0の次」を代入すると
0の次＋（bの次）＝（0の次＋ b）の次

ここで b＝0 を代入すると
0の次＋ 0の次＝（0の次＋ 0）の次・・・④式

ということは③式＝④式になり
1＋1 ＝（0の次＋0）の次・・・⑤式
となる

今度は①式に「a ＝ 0の次」を代入すると
0の次＋0 ＝ 0の次・・・⑥式
となり

⑤式に⑥式を代入すると
1 ＋ 1 ＝（ 0の次）の次

「（0の次）の次」＝「１の次」は2と定義されているので、
1＋1＝2
となる
【証明終了】

※この「（0の次）の次」と書き表せないと、2という「数」であることが言えない
　０以外の数に置き換えるときは、常に「（（（0の次）の次）の次）の・・・」などとなるようにしなければならない

（お疲れ様でした…汗）
（ひとまず休憩しましょう）
（ここからは数学界に根幹を揺るがす衝撃が起こったというお話）

数学の基礎を考え始めた19世紀
数学という構造に穴（矛盾）がないよう、基礎を体系的に完璧に証明しようとする取り組みが始まった

ダフィット・ヒルベルト（1862ー1943）
現代数学の父
完全で無矛盾な数学を目指す「ヒルベルトプログラム（※）」を提唱

バートランド・ラッセル（1872−1970、イギリス）
ノーベル文学賞を受賞した万能の天才
1902年
「数学の基礎固めには十分気をつけなければ矛盾が紛れ込む可能性がある」ことを発見

この「ラッセルのパラドックス」とは
例え話で説明すると、
ある村に1軒の散髪屋があったとする
散髪屋の店主（男性）が
「自分で髭を剃らない村の男性全員の髭を必ず店主がお剃りします。
　自分で髭を剃る男性の髭は店主は剃りません。」
と言っている
ここで「散髪屋の店主自身の髭は誰が剃るのか」という問題が生じる
自分で髭を剃らない場合、店主が髭を剃ることになっているので「自分で髭を剃らない」ことに反する
自分で髭を剃る場合、店主が剃ることになり、「店主は髭を剃りません」に反する
ここで「自分自身を除く」などという例外を作ってしまっては完全性を失ってしまうので、
この矛盾はどうすることも出来ない

このようにヒルベルトプログラムには「自身が破局をもたらすような効果」をはらんでいることが明らかになってしまった

しかし、数学者たちは協力し合って
様々な問題をうまく回避できる方法に辿り着いていく
その一つが
「ZFC公理系」
エルンスト・ツェルメロ（1871ー1953）とアドルフ・フレンケル（1891−1965）が提唱

しかし、様々な回避法を考えていた矢先に決定的な一撃が起こってしまう…

クルト・ゲーデル（1905ー1978）ウィーン大学
アリストテレス以来の大天才と呼ばれ、数学・論理学の巨人
25歳の時にとんでもない事実を証明し、世界中の数学者たちを震撼させた
それは
「‘’初等的な自然数論‘’をふくむω無矛盾な公理的理論は不完全である」・・・（第一不完全性定理）
つまり、
「数学をどれだけ慎重に基礎を固めたとしても、決して証明出来ない難問が必ず存在する」
ことを証明
それはヒルベルトの完全無欠の理論体系を作ることは不可能であるということ
仮に完全無欠であったとしても、その中には証明出来ない難問も必ず存在するということであり、完全無欠かどうかが分からない

証明出来ない難問が数学には存在することを知った数学者たちは、
自分が今取り組んでいる研究が時間の無駄になるのではないかということを疑わなければいけなくなってしまった

ゲーデルの不完全性定理および完全性定理は、数学界のみならず哲学や思想など幅広い分野に大きく影響を与えるものになった

（次回へ続く…？）

最後まで読んで頂き、誠にありがとうございます。
またいつでもいらしてください。

その他のお話

笑わない数学（シーズン２）「バーチ・スウィンナートン＝ダイアー予想」のまとめ

2023.12.17

テレビ番組

笑わない数学（シーズン２）「1+2+3+4+…＝－1/12（無限級数）」のまとめ

2023.12.09

テレビ番組

笑わない数学（シーズン２）「ケプラー予想」のまとめ