笑わない数学（シーズン２）「バーチ・スウィンナートン＝ダイアー予想」のまとめ
笑わない数学（シーズン2）「コラッツ予想」のまとめ
kikorikori
記事内に商品プロモーションを含む場合があります
今回のテーマは「コラッツ予想」
この予想を考えたのはドイツの数学者
ローター・コラッツ（1910ー1990）
ミレニアム懸賞問題（※）の一つ
「全ての数は
偶数なら2で割る
奇数なら3倍して1たす
を繰り返すと必ず1になる」
というもの
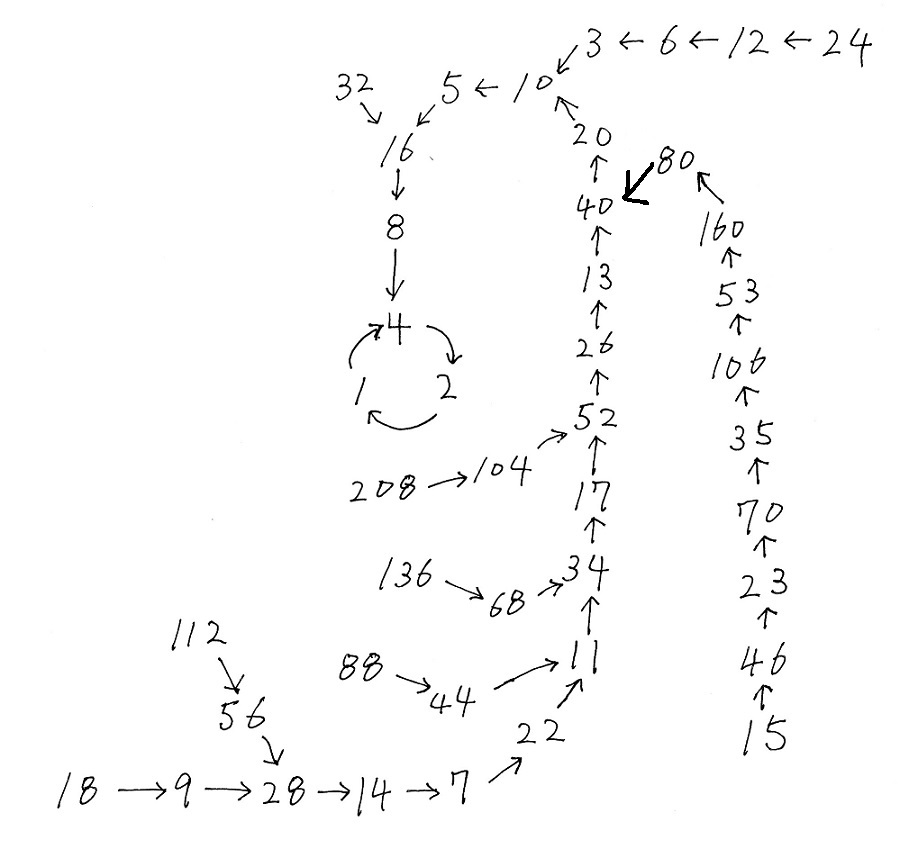
（図中は1～18までは連続しているが、その先は飛び飛びの数になっている）
偶数は自分自身の数より小さくなっていくので、
全ての奇数が1になることが証明できればいいのでは？
なんて思ってしまう…
しかし、偶数を2で割って奇数になることもある
（例えば、6は3。10は5。14は7など）
つまり全ての偶数が1になることを証明するには
結果的に偶数も奇数も1になることを証明しなければならない
さきの発想は2の乗数（2の2乗、3乗、4乗…）のときの偶数なら簡単に証明できる
この予想の正しさは
8垓5777京3599兆4274億9415万144までは確認されている（2023年9月時点）
数学の恐ろしいところはこの予想が正しいように思えても、
実際のところは正しいかどうか分からないし、
正しかったとしても証明可能なものかも分からない
そういった怖さを知りつつも挑戦してしまうのが人間の性（さが）である
コラッツ予想に挑戦していた数学者たち
スタニスワフ・ウラム（1909−1984）ロスアラモス研究所
角谷静夫（1911ー2004）イエール大学 名誉教授
など
現代の数学者たちの多くは敗北宣言をしている
リチャード・ガイ（1916−2020）カルガリー大学 教授
「この問題を解こうとしてはダメだ！」
ポール・エルディシュ（1913−1996）プリンストン高等研究所
「現代数学にはこの種の問題に挑むための準備がまだ出来ていない」
ジェフリー・ラガリアス（1949−） ミシガン大学 教授
「この問題は異常なほど難しく、現在の数学では歯が立たない」
1990年代
ここで変わった方法で挑戦した数学者たちがいた
リホ・テラス と コーネリアス・エベレットは
「全ての数」を「ほとんど全ての数」に限定し、
確率論のテクニックを使用
その結果、「必ず自分自身より小さくなる」
ことを証明した
これは山を登るためにはまず足がかりとなる場所を見つけなければ登頂することは出来ない
二人の証明は登頂する上で大きな一歩を踏み出したと言える
フェルマーの最終定理のように別の予想を証明することで定理が証明できたりするかもしれないし、
ポアンカレ予想のように物理学の世界で利用されていた考え方が必要だったりするかもしれない
そして
ジャン・ポール・アリューシュ（フランス国立科学研究センター 名誉主任研究員）によって
「ほとんど全ての数は
偶数なら2で割る
奇数なら3倍して1たす
を繰り返すと
必ず自分自身の0.869乗よりも小さくなる」
ことを証明
続いて
イバン・コレック（スロバキア科学アカデミー 主任研究員）によって
「ほとんど全ての数は
偶数なら2で割る
奇数なら3倍して1たす
を繰り返すと
必ず自分自身の0.7925乗よりも小さくなる」
ことを証明
2019年
テレンス・タオ
偏微分方程式（解析学）の手法を用いて
「ある意味好きなだけ自分自身よりも小さくなる」
ことを証明
もしかしたら、2050年までに証明される日が来るかもしれない
（次回に続く）
※ミレニアム懸賞問題
2000年にアメリカにあるクレイ数学研究所が、21世紀で解決すべき重要な難問として100万ドルの懸賞金をかけた７つの問題（そのうち１つはポアンカレ予想でグレゴリー・ペレルマンが解決済み）
P≠NP予想
理論計算機科学の難問
ポアンカレ予想 （グリゴリー・ペレルマンによって解決済み）
位相幾何学分野の難問
宇宙の広がりとの関係性など
リーマン予想
素数と深い関係がある
ヤン-ミルズ方程式と質量ギャップ問題
素粒子の謎について
ナビエ–ストークス方程式の解の存在と滑らかさ
物理学分野の流体についての解
飛行の理論にも影響
バーチ・スウィンナートン＝ダイアー予想（BSD予想とも）
数論分野の難問
ホッジ予想
代数幾何学分野の難問
最後まで読んで頂き、誠にありがとうございます。
またいつでもいらしてください。
その他のお話
笑わない数学（シーズン２）「1+2+3+4+…＝－1/12（無限級数）」のまとめ
笑わない数学（シーズン２）「ケプラー予想」のまとめ
笑わない数学（シーズン２）「超越数」のまとめ
笑わない数学（シーズン２）「結び目理論」のまとめ
笑わない数学（シーズン２）「1＋1＝2」が正しい理由のまとめ
笑わない数学（シーズン2）「コラッツ予想」のまとめ
笑わない数学（シーズン2）「非ユークリッド幾何学」のまとめ
