笑わない数学(シーズン2)「バーチ・スウィンナートン=ダイアー予想」のまとめ

For English notation, please use the orange translation function in the upper right.
今回のテーマは「バーチ・スウィンナートン=ダイアー予想」
これは数学者の
ブライアン・バーチ(1931ー、イギリス)
と
ピーター・スウィンナートン=ダイアー(1927ー2018)
の2人の名前の頭文字をとって「BSD予想」とも呼ばれてる
このBSD予想はアメリカのクレイ数学研究所が2000年に発表したミレニアム懸賞問題の一つ
今までにミレニアム懸賞問題では
リーマン予想
ポアンカレ予想
P≠N P予想
ナビエーストークス方程式
を取り上げてきた
今回のテーマがそれらの中に含まれるということは、
数学にとって難しいだけでなく、めちゃくちゃ重要な問題だということ
今回の目標は、「BSD予想とは一体どんな難問なのか」をざっくり理解することにする
しかし、いきなりBSD予想の説明をするにはかなり困難を極めるので、
まずは簡単なものからやっていくことにする
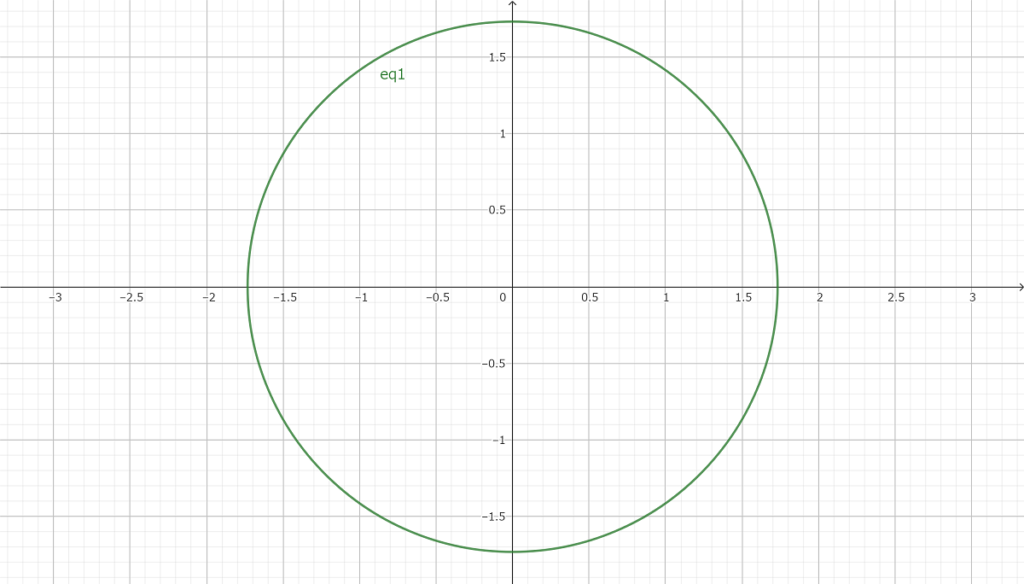
以下は円の方程式とそのグラフである
x2+y2=2
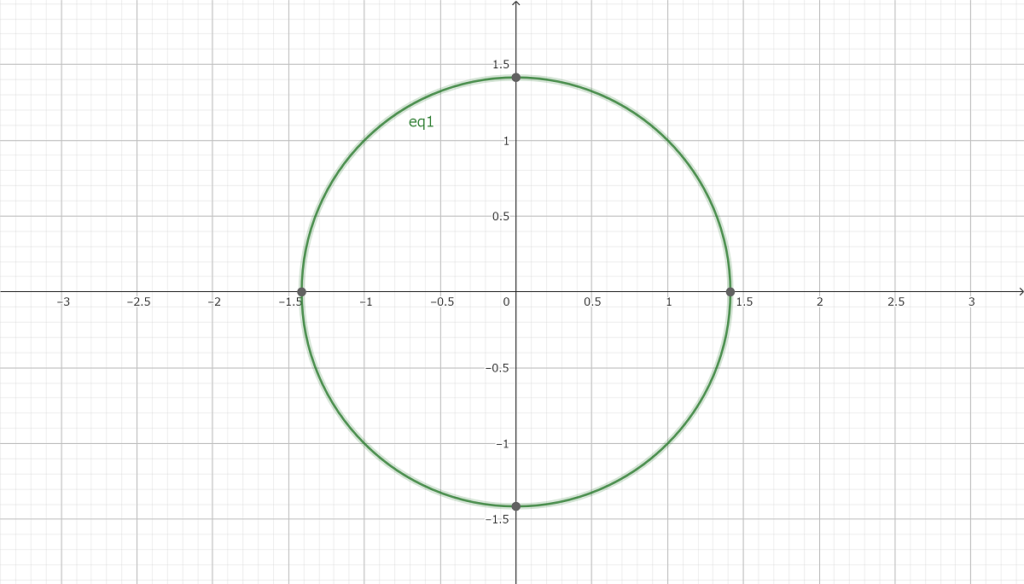
このグラフ上の点で整数になる点を探してみる
すると
(1、1)(−1、1)(−1、−1)(1、−1)
全部で4つ
では座標が有理数になる点は? (有理数とは分数で表せる数)
そうなると途端に難しくなる
だが、これはBSD予想とは何かを理解するためにとても大事なので求め方を解説する
まず、座標が整数になる点を通る直線を考えてみる
例えば、
傾き2の直線
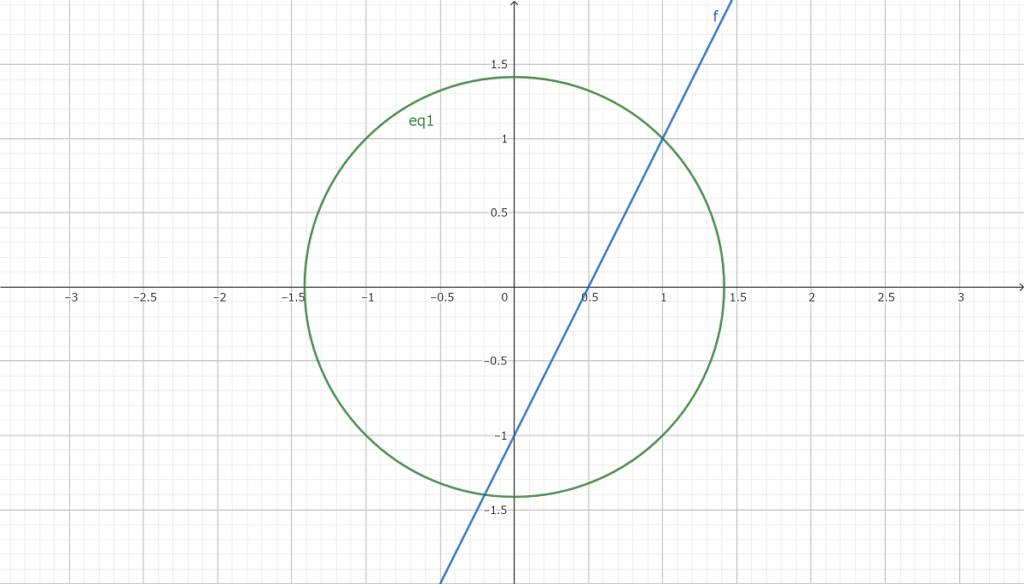
傾き1/2の直線
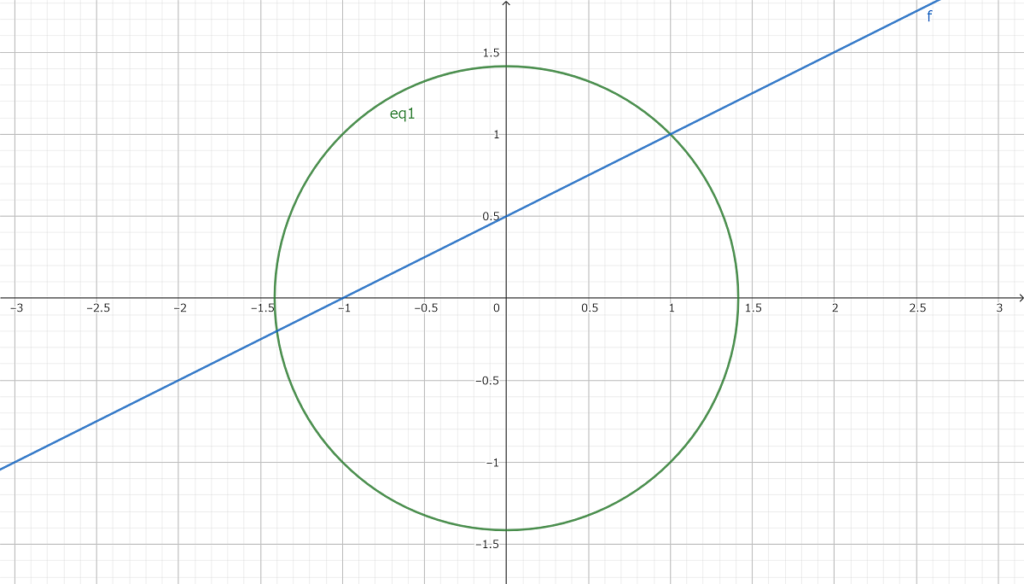
傾き11/7の直線
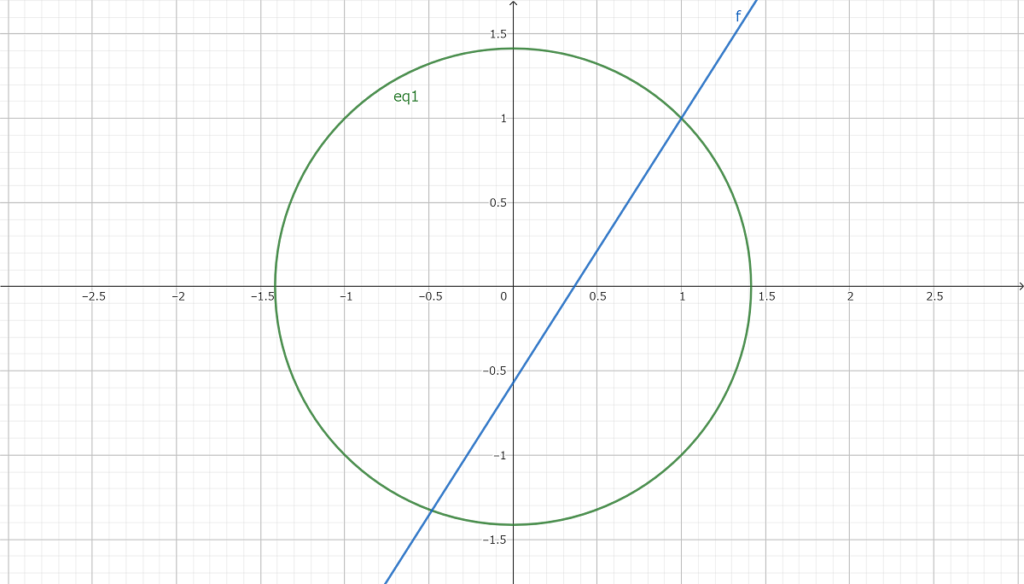
どれも傾きが有理数になっている
実は有理数の傾きの直線が円と交わる点の座標は必ず有理数になっていることが証明されている
有理数の傾きの直線は無限個描くことが出来るので、それと交わる点も無限個ある
こういったグラフ上の点が有理数になる点を求める問題を数学では
「有理点を求める問題」
と呼ばれている
なんだか無限個もあってとても退屈そうな問題だ
しかし、有理点を求める問題は実は古代ギリシャに誕生して以降
フェルマーやオイラー、ガウスなど数々の天才たちを夢中にさせた数学史上の一大テーマなのである
数学史に詳しい
マーカス・デュ・ソートイ(1965ー、オックスフォード大学数学研究所教授)
有理点を求める重要さをこう語っている
「私たち数学者は現在に至るまで2000年もの間、有理点の問題に夢中になってきました。
有理点の問題は決して何かの役に立つ訳ではないものの数学の新しいアイデアをもたらす源
となってきたからなのです。」
それだけ有理点を求めることは数学にとって非常に重要なことなのである
次に考えるのはさっきより一回り大きな円x2+y2=3について
x2+y2=3に有理点がないことを証明せよ
背理法を使って証明する
仮定:x2+y2=3に有理点があるとする
有理点があるのだから
x=A/C、y=B/C
と分数で表すことができる
ここで大事なのは
A、B、Cは同時に同じでは割り切れない(互いに素)ということ
それぞれxとyに代入して、式を整理すると
A2+B2=3C2
ということは、A2+B2は必ず「3の倍数」になっているはずである
するとAもBも「3の倍数」でなければならない
そこから、Aが「3の倍数」ならA2は「9の倍数」になる
Bも同様である
このことから、A2+B2は「9の倍数」になる
イコールで結ばれている3C2も当然「9の倍数」になる
3C2=9の倍数
両辺を3で割って
C2=3の倍数
となり、
元のCも「3の倍数」
ここでA、B、C全ての数が「3の倍数」になってしまい、
同時に同じ数で割り切れないということに矛盾が起きてしまう
ということはそもそもの仮定が誤りなので、
x2+y2=3に有理点は一つもない
ということになる
こっちの円には有理点が無限個あるが、
こっちの円には有理点が一つもない
一体どんな円なら有理点があって、どんな円なら有理点がないのか・・・
フォルマーやオイラーなどの数学者たちは18世紀頃までに円を含む円錐曲線の有理点を徹底的に調べて明らかにしていった
アイザック・ニュートン
ピエール・ド・フェルマー
クロード・パシェ
・
・
・
それでも「有理点を求める問題は地味でパッとしない」なんて思う人もいるはず
実は有理点を求める問題は『めちゃくちゃ×3』 すごいことにつながっている
ルイス・モーデル
アンリ・ポアンカレ
カール・フリードリヒ・ガウス
レオンハルト・オイラー
・
・
・
数学者たちはその後、さらに難しい曲線の有理点を求める問題に挑み始めていった
その曲線とは「楕円曲線」
この楕円曲線の有理点を求める問題がBSD予想につながっている
楕円曲線とは何か
こんな感じのぐにゃりと曲がった曲線が楕円曲線
y2=x3-2x
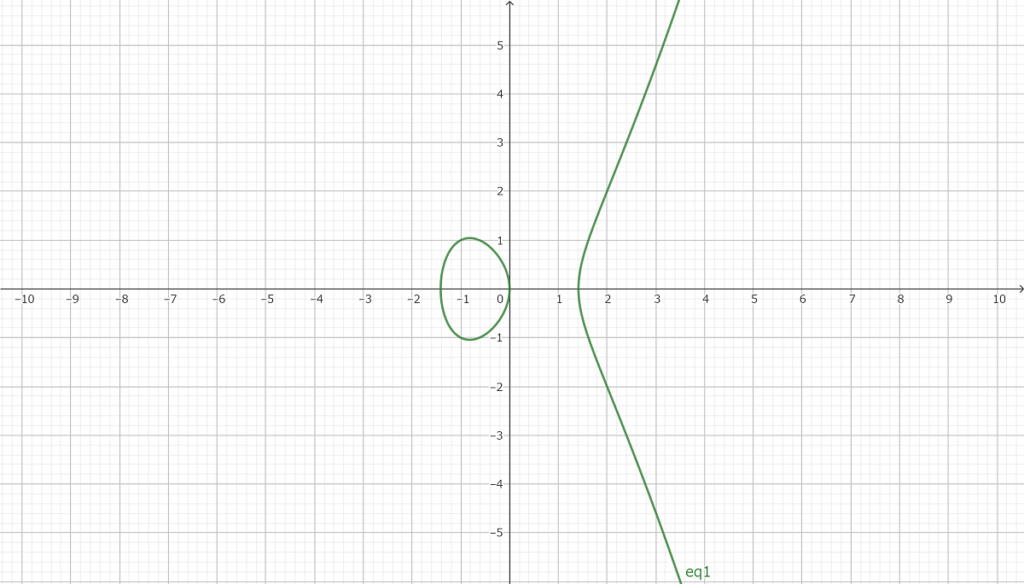
y2=x3+1
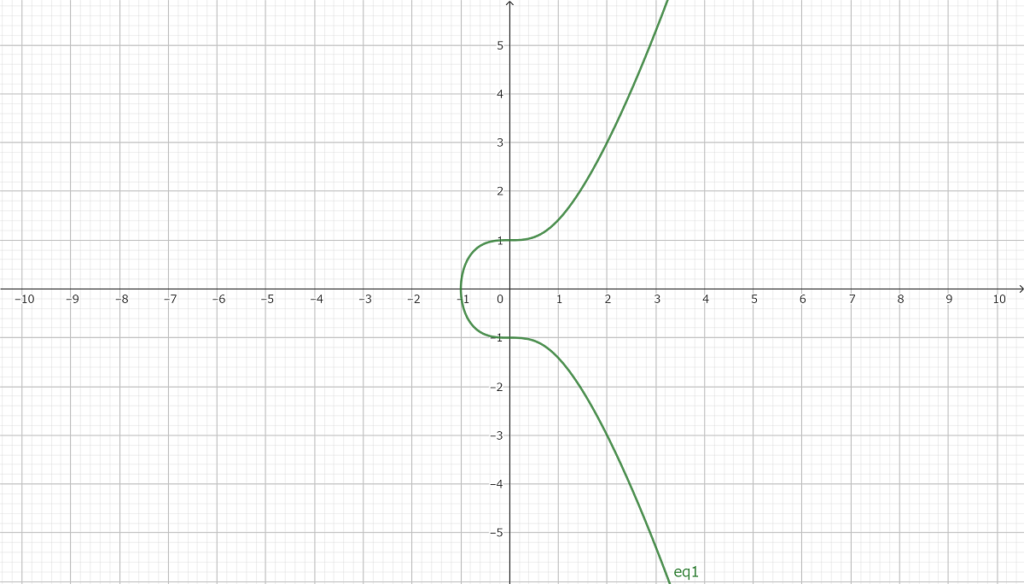
y2=x3-x+1
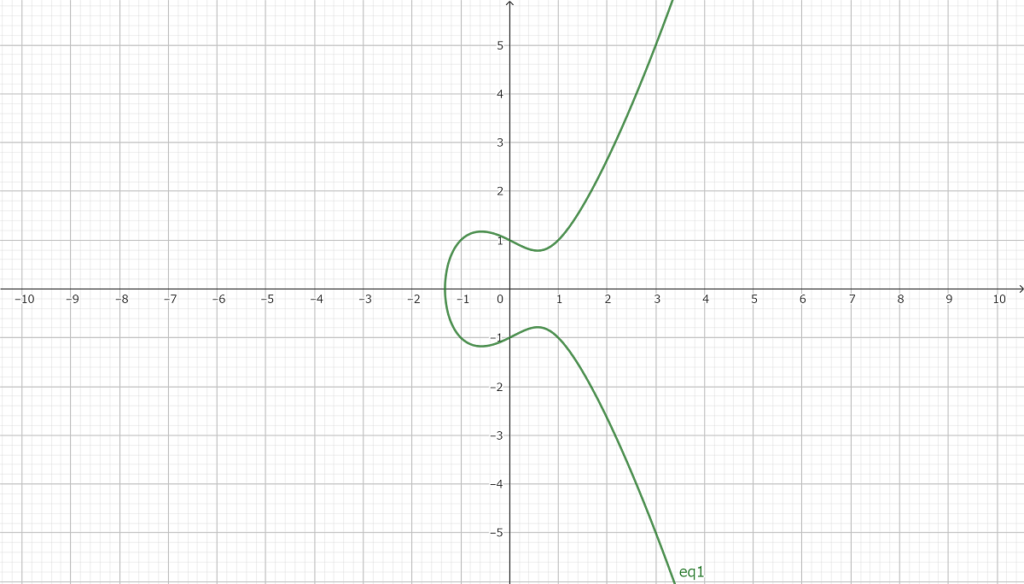
この楕円曲線の上の有理点の個数が現代数学の一大テーマになっている
それでは楕円曲線の有理点を探してみることにする
まずはこれ
y2=x3+1

このグラフの上の有理点はどこかというと…
(0、1)(−1、0)(0、−1)
この3つの点が有理点であること分かる
だが有理点は他にもまだまだある
そこで分かっている有理数からまだ分かっていない有理点を見つける方法がある
その方法とは
すでに分かっている二つの有理点を
直線で結び、再び楕円曲線と交わる点を求めると
不思議なことにその点も有理点になっているという性質がある
その座標は計算すると
(2、3)(2、ー3)
これで答えは5個
この楕円曲線についてはこれが全てだということが分かっている
別の楕円曲線の有理点も探してみましょう
y2=x3+2
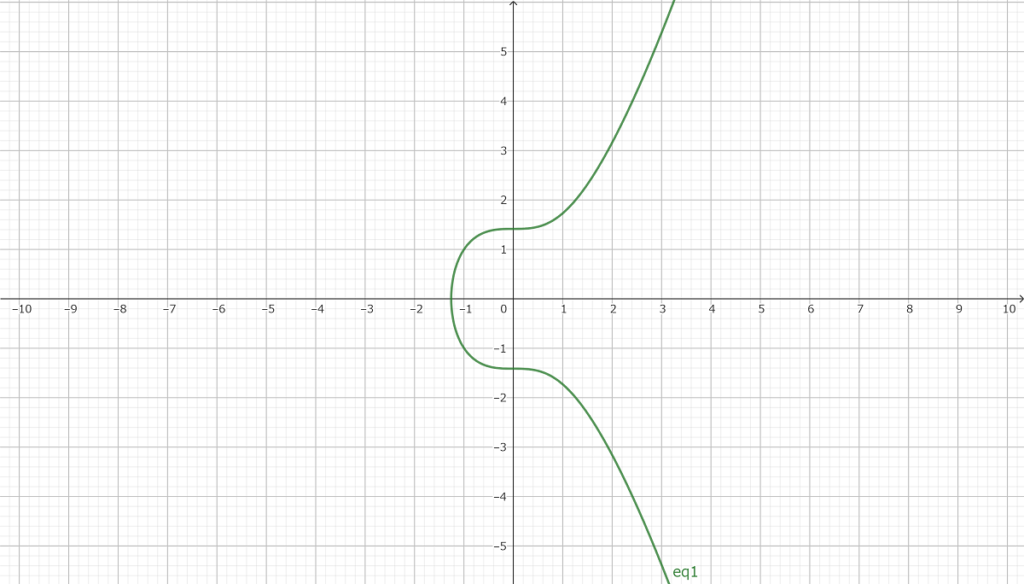
これは
(−1、1)(−1、−1)
という有理点がすぐに見つかる
さっきと同じように二つの点を結ぶと
この直線は楕円曲線と交わらないので
新たな有理点を見つけるにはまた別の方法を使うしかない
そんな時は分かっている有理点に接線を引いてみる
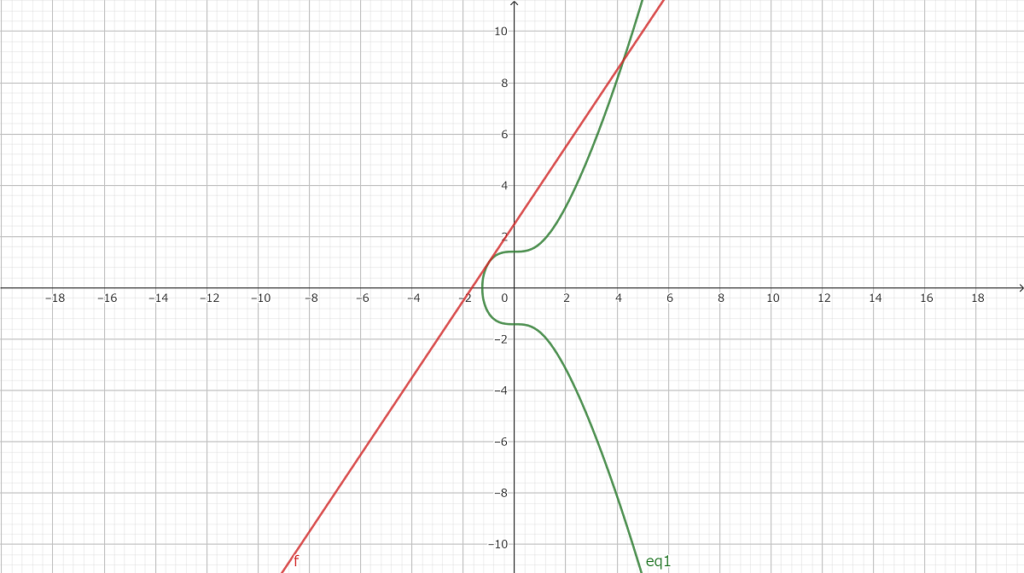
接線を伸ばしていって、楕円曲線との交点を求めると…
実はその点も有理点になっているという性質がある
この場合、ちゃんと計算すると…
座標はちょっとややこしい有理数だが
(17/4、71/8)
この新たな有理点が見つかったことで
次から次へと芋蔓式に有理点が見つかっていく
この新たな有理点と(-1、-1)の点を結んだ直線と楕円曲線との交点も有理点
(127/441、13175/9261)
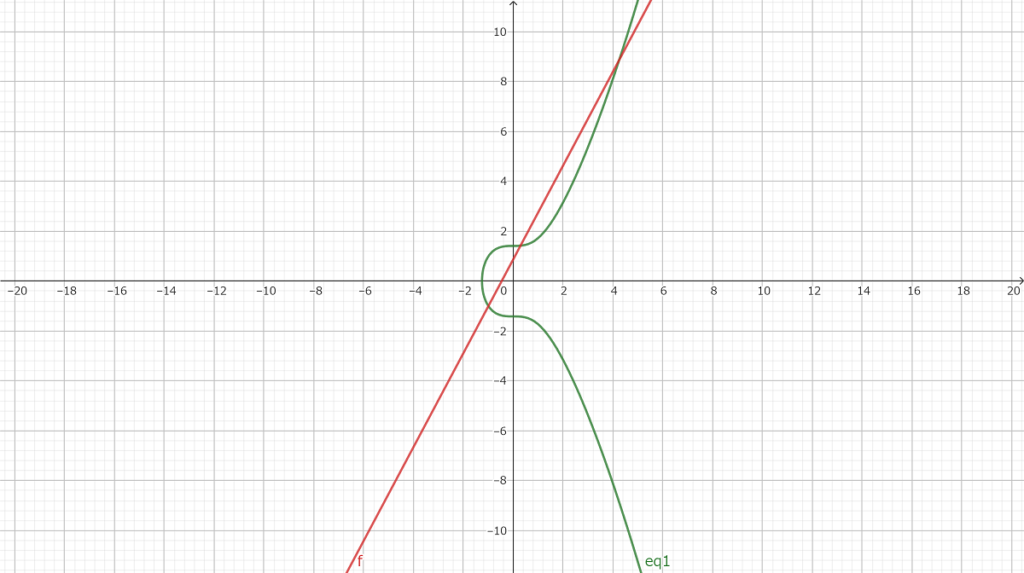
その新たな有理点と(-1、1)の点を結んだ直線と楕円曲線との交点も有理点
(66113/80656、36583777/22906304)
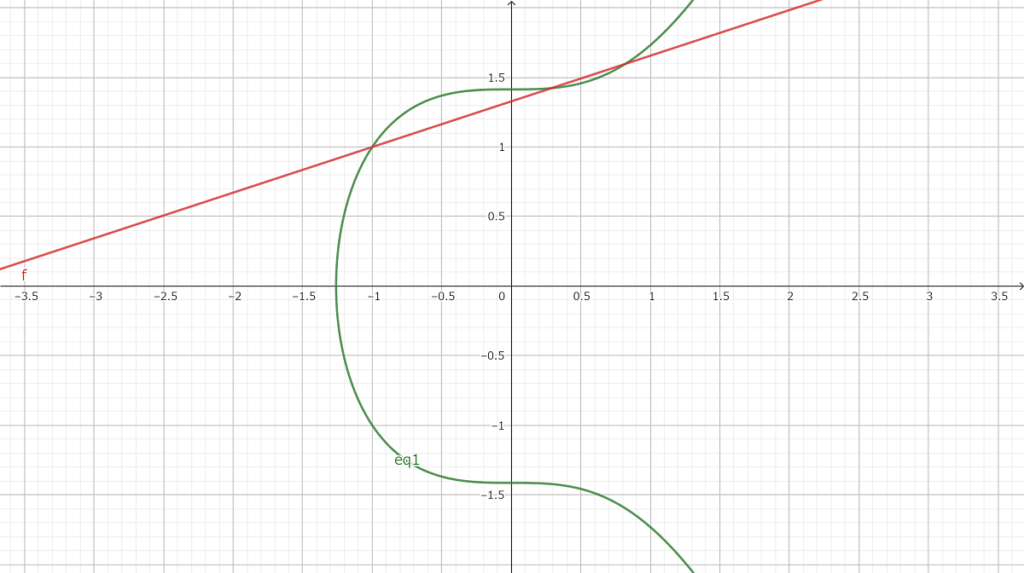
その新たな有理点と(-1、-1)の点を結んだ直線と楕円曲線との交点も有理点
(108305279/448846121、1226178094681/341385539669)
出てくる数字がややこしい有理数ばかりですが、これが無限に続いていく
なので、この楕円曲線は有理点が無限個あることが分かる
今度は別の楕円曲線について調べてみる
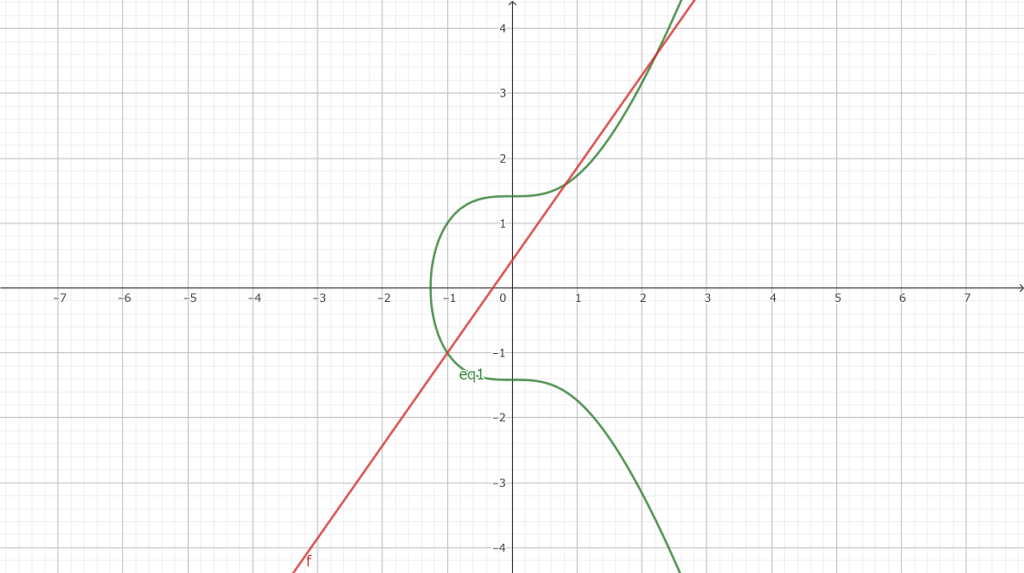
y2=x3+17
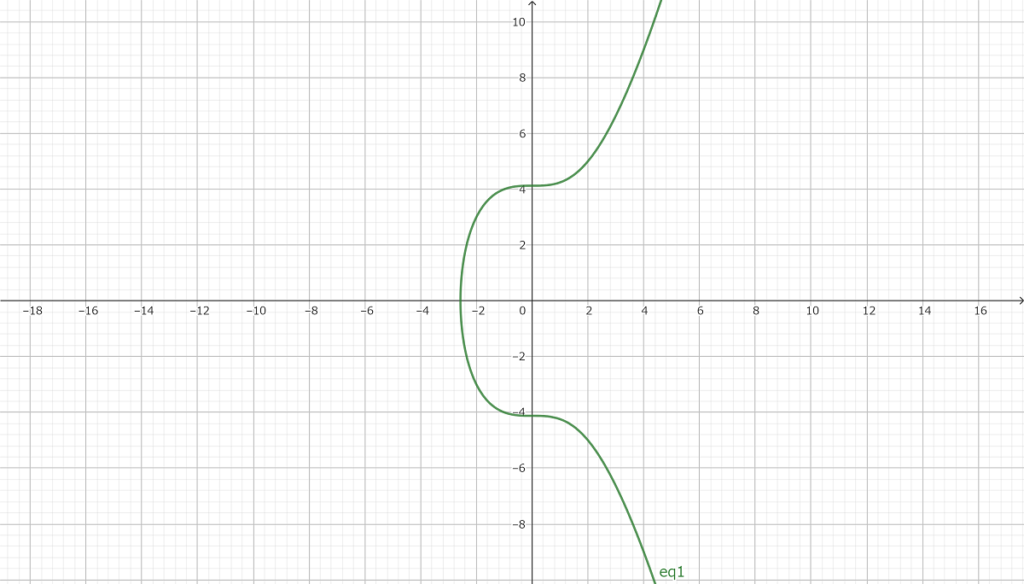
すぐ見つかる有理点はこの2つ
(−1、4)(−1、−4)
さっきと同じように(−1、4)の点に接線を引いて有理点を見つけていくと
まずこの有理点が見つかって
その有理点から次の有理点が見つかって
・
・
・
こんな感じがずっと続いていって
やはり無限個の有理点があることが分かる
ところがこの楕円曲線には
これとは別に無限個の有理点がもう1セットある
さっきは(−1、4)を出発点にしたが、
(4、9)を出発点にすると…
さっきの有理点とは全く別の有理点のグループがあって、
・
・
・
それも無限個あることが分かる
つまり、この楕円曲線には無限個の有理点のグループ
(−1、4)のグループ と (4、9)のグループ
の2セットがある
それは無限個×2の有理点があるということになる
ふ〜
今回はいつも以上に難解だ
ここで一休み
BSD予想とは何かまであと少しなので頑張ろう
ここまでで楕円曲線には有理点が無限個ある場合があるのだが、
その無限個にも無限個×1であったり、無限個×2であったりすることが分かった
実は無限個×3や無限個×4の有理点を持つ楕円曲線もある
でも、ある楕円曲線があったとき、
その有理点が無限個×?になるかは調べればすぐに分かると思うかもしれない
ところが、実はこれがめちゃくちゃ難しい
例えば、
無限個×3の楕円曲線が初めて見つかったのは1938年
無限個×4は1945年
無限個×5はなんと・・・
1986年まで見つからなかった
つまり、ある楕円曲線があったとき
その有理点の個数は無限個×?の『?』が何なのかをすぐに分かる手段が全くなかった
と、ここまできたら
勘の鋭い人ならBSD予想が何なのか分かってきたかもしれない
そう、
バーチとスウィンナートン=ダイアーはこの『?』はこうに違いないという予想を
この長い数学史上で初めて打ち立てた!!
1950年代半ば
イギリスのケンブリッジ大学に純粋数学で名を上げたいと燃えていた二人の若手数学者がいた
ピーター・スウィンナートン=ダイアー(1927ー2018)
ブライアン・バーチ(1931ー、イギリス)
のちにBSD予想として知られる数学者のコンビ
BSDのコンビがターゲットとして選んだのが…
当時、超難問として畏れられていた楕円曲線の有理点の謎
つまり、どうすれば無限個×?の『?』が分かるのか
実はこの問題を解くために二人が選んだ方法は世界の誰もが思いつかなかった方法だった
まだ登場して間もなかったコンピューターを使うというものだった
(当時の最先端コンピューターはEDSACⅡ)
BSDの二人は、まず様々な楕円曲線についての基本的な情報をコンピューターで地道に計算することから始めた
そして、その情報をさらにコンピューターに入力して計算し、その結果をコツコツとグラフに記入し続けた
かかった時間は実に6年!
そして、ついにそのグラフの傾きを表す数値があの『?』にぴったり当てはまるようだという
誰も想像出来なかった事実に辿り着いた
2人の結論を数学の言葉で書くとこうなる
「xより小さい全ての素数pについて、Np/pを掛け合わせたものは定数C×logXのr乗に
漸近するはずだ」
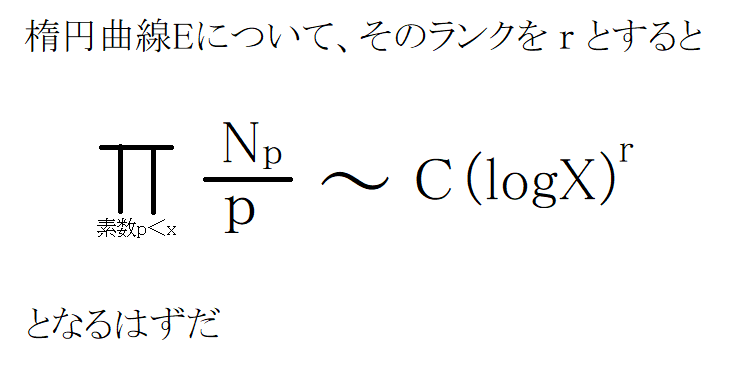
これはさっきの『?』がこんな感じの式で求められるはずだというもの

数式はめちゃくちゃ難しいですが、これがBSD予想の誕生だった
マーカス・デュ・ソートイ(1965ー、オックスフォード大学数学研究所教授)
「BSDの二人が楕円曲線の有理点の謎であった無限個✖️?の?を簡単に見分ける方法を発見した
ことは大きな驚きでした。数学者たちが2000年も行き詰まっていた問題に全く新しい視点を
与えたのですから。数論において実に革命的な瞬間でした。」
今回の目標であったBSD予想とは何かにやっと辿り着いた
今、あなたは数学の一つの最先端に立っている(2023年時点)
そんな感覚を少しでも感じとってもらえたら嬉しい
しかし、意外な事実がある
21世紀に入ってBSD予想について誰も予想しなかったことが分かってきた
それは数学者にとって、真っ先に挑まなくてはならないほどの重要な問題が元々BSD予想には含まれていた!
という驚きの事実だった
(まだこのブログではまとめていませんが…汗)
笑わない数学(シーズン1)第一回で取り上げた「素数」
その素数について並び方に規則性はあるのかという大きな謎があった
さらにその謎が宇宙を支配する自然法則とも繋がっているのではないかという意外な事実も紹介した
その素数の謎を解き明かす鍵を握っているのが「リーマン予想」と呼ばれるものだった
実は今回紹介したBSD予想はこのリーマン予想をはるかに上回る新たな予想
『深リーマン予想』
とも呼ばれるものにつながっているという事実がつい最近明らかになってきた
もし深リーマン予想やさらにその先に続く謎が解き明かされれば、
素数の並び方の謎をより深く解明出来るだけでなく、
双子素数の謎やゴールドバッハ予想などさらなる謎が解ける可能性が出てくると言われている
つまり、有理点を突き詰めたBSD予想の先にこそ数学者たちが長年追い求めてきた
「数とは何か」
そして、
宇宙の自然法則の真の姿が隠されているのかもしれない
BSD予想…
最初はめちゃくちゃ地味でつまらない話だと思っただろうか
それが今となっては、
「マジ有理点すげ〜」とか慌ててたり?
数学とはそれがどんな分野でも常にとてつもないふか〜い世界へとつながっているもの
今回そのことが少しでも伝わったなら、すごく嬉しい!
さて、シーズン1とシーズン2を通じて全20回
シーズン2でも脳みその糖分がすっかり無くなってしまった(空)
「では、またどこかで…
数学にサンキューーーーーーーーーーー!!」(パンサー・尾形貴弘【1977ー】)
尾形さん、スタッフの皆さん本当にお疲れ様でした!!
(おしまい)
最後まで読んで頂き、誠にありがとうございます。
またいつでもいらしてください。
その他のお話








