2023.12.09 2024.05.26

笑わない数学（シーズン２）「1+2+3+4+…＝－1/12（無限級数）」のまとめ

kikorikori

記事内に商品プロモーションを含む場合があります

今回のテーマは「1+2+3+4+…＝－1/12」

これはインチキか？
足していくはずなのにマイナスなんてあり得ない
そう思う人がほとんどだろう

いきなり本題の数式を解説する前に次の数式を考えてみる

1＋1／2＋1／4＋1／8＋1／16＋・・・＝？

この数式も無限個の数を足していく（マイナスも含む）
こういった数が数学の世界ではしょっちゅう登場する
こんなモンスターのような数であっても、うまくねじ伏せる方法を数学者たちは確立していく

まずはいきなり無限個を足すのではなく、
100番目までの和を考えることから始める

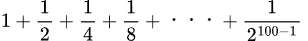
と表せることが分かる

この合計をS₁₀₀と表す

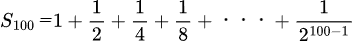
次にこの式を2倍した数を考えてみる

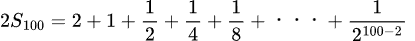
2S₁₀₀とS₁₀₀を見比べてみると共通する数が多い

2S₁₀₀からS₁₀₀を引いてみる

すると

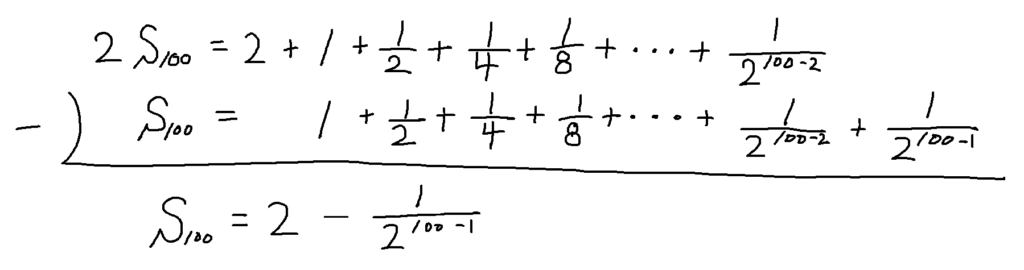
S₁₀₀は100番目までの和なので

無限番目までは

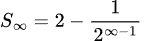
となり、

2^∞ー1はものすごく大きな数になっていくので、

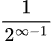
は限りなく0に近づくことになる

ということは・・・

求めたかった無限番目までの和は「2」ということになる

正体不明に思えたモンスターもちゃんと答えが求まって一安心できたと思う

こういった無限個の和で表す数を無限級数という
この無限級数には色々な種類がある

ではこの2つの無限級数はどうか
　　1+2+3+4+・・・＝？
　　1-2+4-8+・・・＝？
きちんと調べてみる

まずはこの無限級数から
1+2+3+4+・・・＝？

n番目までの和は

で表される

ということは・・・

無限番目までの和は

ということになり、無限に大きくなっていく

無限は数とは認められていないので

この無限級数は　答えなし　になる

次はこの無限級数

1-2+4-8+・・・＝？

n番目までの和は

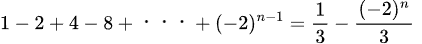
で表される

ということは

無限番目までの和は

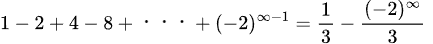
となり、（−2）^∞／3はプラス無限になったり、マイナス無限になったりして

一つの答えにまとまることはない

ということで、やはりこの無限級数も　答えなし　になる

このように答えのない無限級数を
発散する
という

逆に答えがある無限級数は
収束する
という

無限級数には答えがあるもの（収束）と答えがないもの（発散）の2種類がある
数学なのに答えがないのは残念だと思うかもしれない
しかし、現代数学では発散する無限級数は和を考えることに意味はないとされている

この結論に至るまで数学者たちは何とかこのモヤモヤを解消する方法はないかと考えていた時代があった

18世紀初頭のイタリア
修道士でもあった数学者
ルイージ・グイード・グランディ（1671ー1742）
1−1＋1−1＋・・・の無限級数について考えていた
現代数学では、1と0を行ったり来たりするので答えはないとされるもの
しかし、グランディが辿り着いた結論はなんと・・・

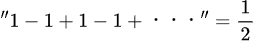
であった

1710年に発表した著書の中でその理由を例え話でこう書き記している
「ある兄弟が親から一つの宝石を相続することになった。
　遺言で売却を禁じられていたため、2人は交互に宝石を保管することにした。
　2人はそれぞれ半分の時間を保管しているため、これが無限に続くと考えると
　これを1／2ずつ所有しているということになる」

答えがないはずの無限級数にも何とか答えを与えたいと思う数学者は他にもいました

クリスティアン・ヴォルフ（1679ー1754）
1−2＋4−8＋16−32＋・・・を考えていた
この無限級数はn番目の和が

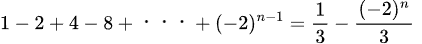
になる
これは
nが大きくなっても変わらない部分「コア」
nが大きくなっていくと発散してしまう部分
とに分かれる

発散する部分は平均すれば“ざっくりゼロ”になるので、
発散を無視してコアだけ見ると
1／3
だから、これが答えだと主張した

18世紀半ば・・・

レオハルト・オイラー

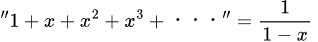
という公式で無限級数について考えていた
ただし、この公式は
−1＜x＜1
この範囲でしか成り立たない

オイラーはあえてこの範囲の外側を利用することで答えがない無限級数でも答えが求められるとした

例えば、
範囲外のx＝−1を無理矢理代入して整理すると
”1−1＋1−1＋1−1＋・・・”＝1／2
と、ブランディが求めた答えが導き出される

さらにx＝−2を無理矢理代入すると
”1−2＋4−8＋16−32＋・・・”＝1／3
と、今度はヴォルフが求めた答えが導き出される

次はこんな公式について考えた

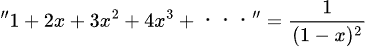
ただし、この公式も
−1＜x＜1
この範囲でしか成り立たない

ここにx＝−1を代入すると

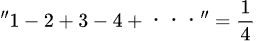
となり、
答えがないとされた無限級数にも答えはあると発表
数学界を驚かせた

このことから
1＋2＋3＋4＋・・・　＝ー1／12
が正しいとする議論もある

まず
A＝1＋2＋3＋4＋5＋6＋7＋・・・
とする

Aの4倍は
4A＝4＋8＋12＋16＋20＋24＋28＋・・・

Aの偶数部分と4Aのそれぞれの数を引くと

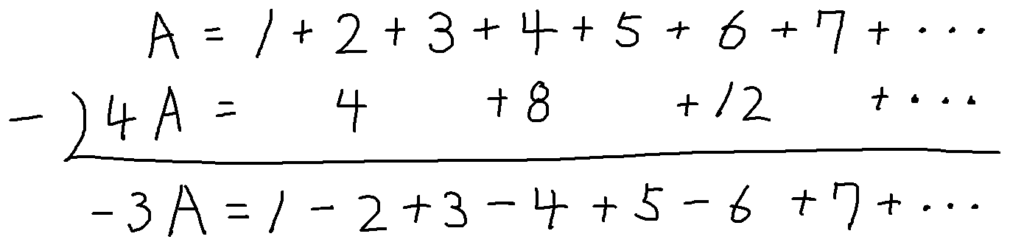
1−2＋3−4＋5−6＋・・・はオイラーによると1／4なので
−3A＝1／4
A＝−1／12

実際には発散するので正確ではないはずである
なぜならこの数学者たちの考えを発展させていくと、
∞＜−1
という議論にまで及んでしまう

19世紀に入ると
発散する無限級数は和を考えることに意味はない
という考え方を採用することにした

それでもしつこく答えを求める数学者たちがいた

1890年代のイタリア・・・

エルネスト・チェザロ（1859ー1906）
発散する無限級数の和を考えることに意味があると主張した
特殊な計算方法「チェザロ総和法」を編み出して計算してみせた

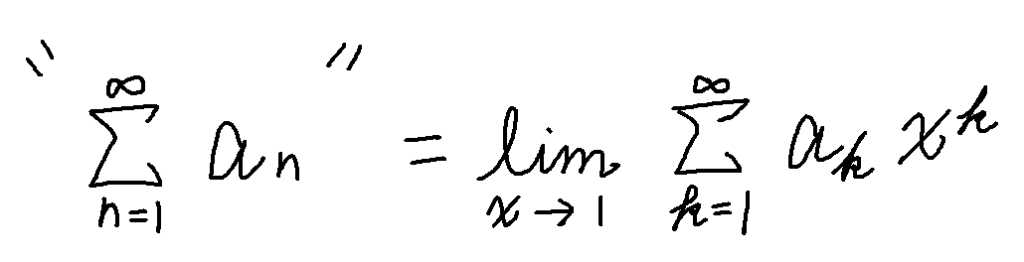
この数式にグランディが考え続けた
“１-１+１-１+・・・”＝？
の無限級数を当てはめて計算してみると

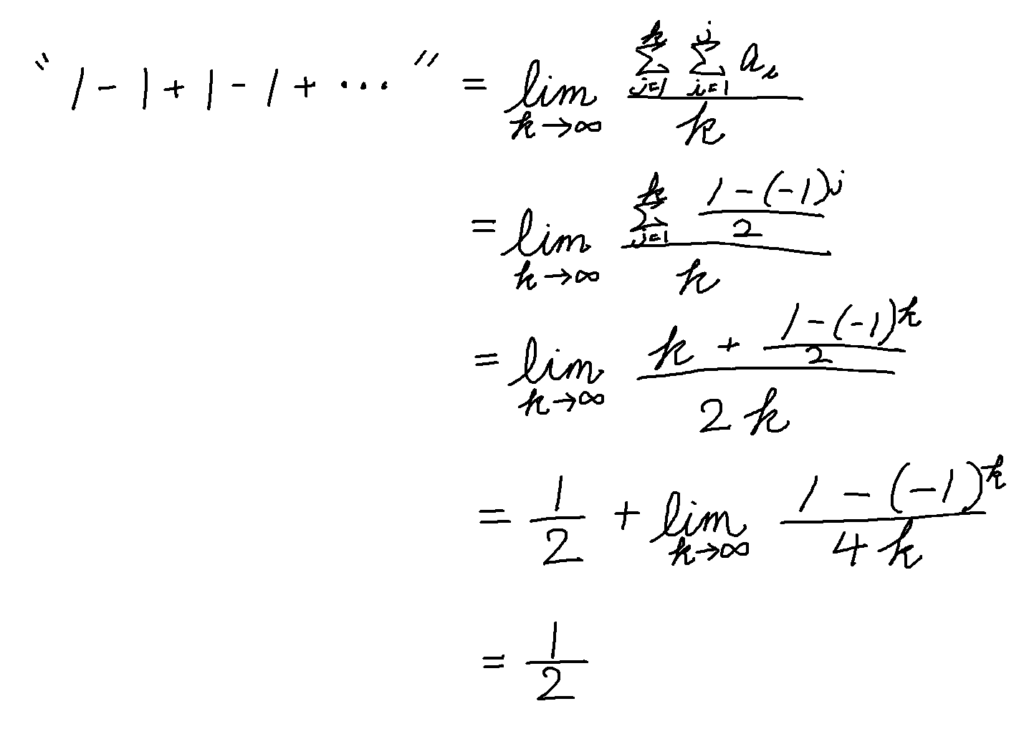
チェザロが考えた方法はかつての数学者たちが議論してきたものを
足し算のやり方を上手い具合調整することで答えを導こうとするもの

さらに他の無限級数でも答えを求められる別のテクニックが登場する

アーベル総和法

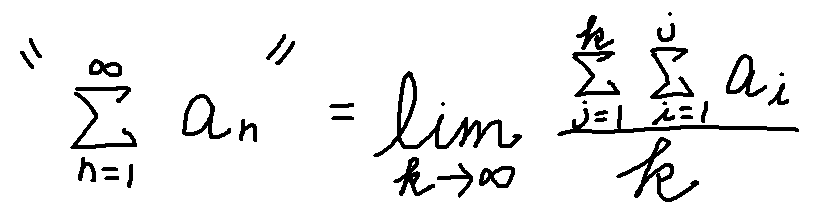
ボレル総和法

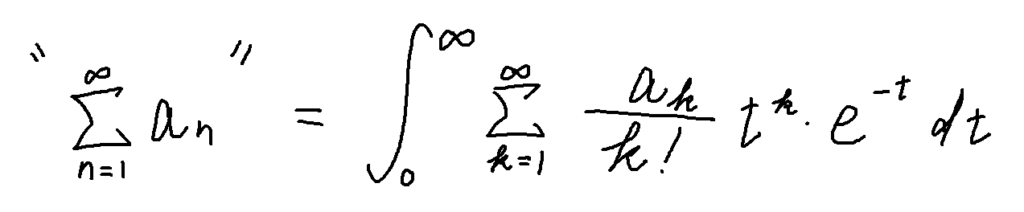
これらの方法を使うと18世紀の数学者たちと同じ結論が出る

そして
“1＋2＋3＋4＋・・・”＝？
も計算できるとする驚きの方法まで登場した

インドの魔術師
シュリニバーサ・ラマヌジャン（1887ー1920）

ラマヌジャン総和法

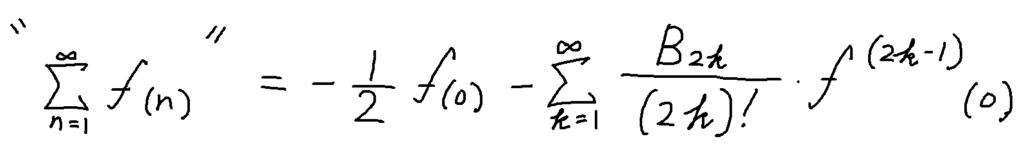
これを使うと
“1＋2＋3＋4＋・・・”＝−1／12
が導き出される

イギリス人数学者・ハーディに宛てた手紙にこんなことを書き記している
「私の理論では“1＋2＋3＋4＋・・・”＝−1／12になります。
　こんなことを言い出したら、先生は私に病院に行けというかもしれませんね」

絶対にあり得ないと思えるこの結論
その真意は一体何なのか

実は解析学のテクニックを使うことで
コアの部分と発散する部分に分離できる
というところが背景にある
そして発散する部分はコアの部分よりある意味重要度が低いため
“1＋2＋3＋4＋・・・”＝−1／12
という考えになるという

ちなみにラマジヌジャンと同じ結論に
他の方法でも辿り着くことができる

その一つでもあるゼータ関数正規化法（素数に深い関係がある）

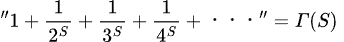
ただし、Sの実部＞1

ここに範囲外の数S＝−1を無理矢理代入することで
”1＋2＋3＋4＋・・・”＝−1／12
が求められる

こうして見ると発散する無限級数の和を考えることに深い意味があるように思えてくる

“・・・“はこの式は“普通とは違う意味” で正しいといえる

そもそも “怪しい和” を求めることに何か実用性のある良いことでもあるのか？
数学者の単なる自己満足では？
そう言いたくなってくる

ところが、
その “怪しい和” を求めることに意味があるかもしれないことが分かった！！

1948年
オランダの物理学者
ヘンドリック・カシミール（1909ー2000）
発表した論文が大きな議論を巻き起こした
極小さな隙間を隔てた2枚の金属板の間にそれまで知られていなかった奇妙な引力が働くはずだ
という予言
のちに カシミール効果 と名付けられた現象
もしその引力が存在するとすれば
その大きさは
“1＋2＋3＋4＋・・・”＝−1／12に比例する（1次元カシミール効果の場合）
実際の3次元の場合、“1³＋2³＋3³＋4³＋・・・”＝1／120に比例
ということが明らかになった