笑わない数学（シーズン２）「バーチ・スウィンナートン＝ダイアー予想」のまとめ
笑わない数学（シーズン２）「ケプラー予想」のまとめ
kikorikori
記事内に商品プロモーションを含む場合があります
今回のテーマは「ケプラー予想」
17世紀の初め
イギリスの軍人が知り合いの数学者に
「船に出来るだけたくさんの砲弾を積み込みたいんだけど、どう積んだらいいか？」
と持ちかけたことが発端だった
これは
「箱にピンポン玉を最もたくさん詰め込むにはどうしたら良いか？」
ということに等しい
平面上では円と円のくぼみの間に円を敷き詰めていくのが、最も効率が良いはずである
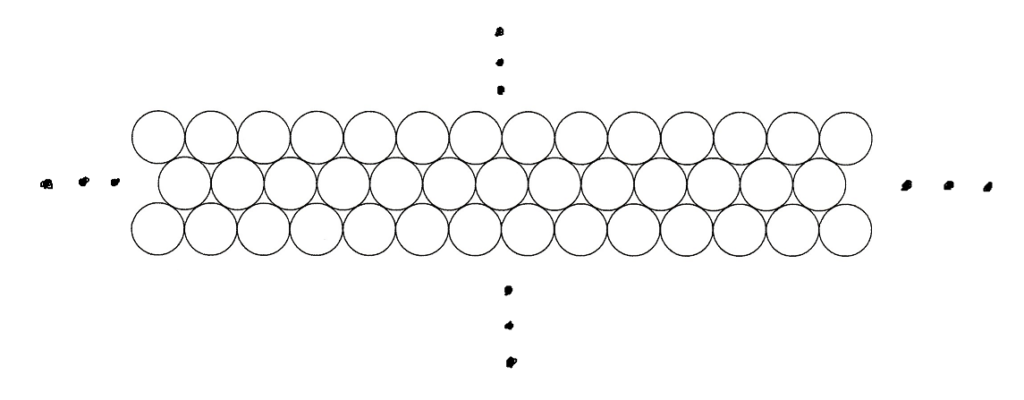
立体的に考えると、三つの球のくぼみに球を置いていくのが、最も効率が良いはずである
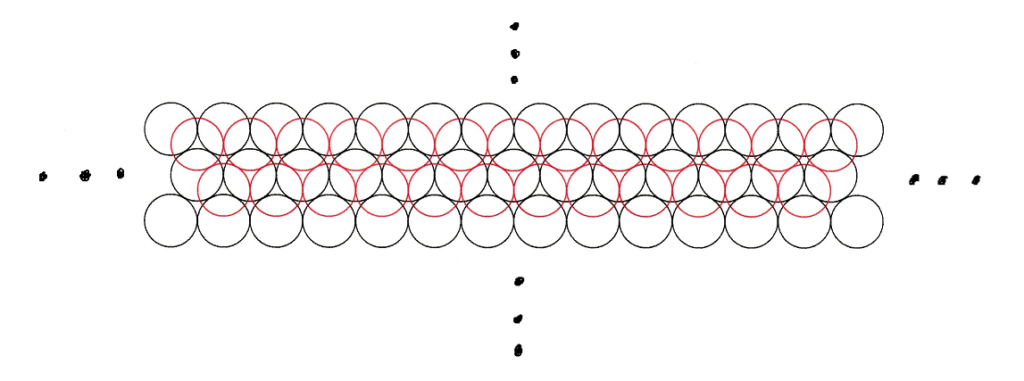
ケプラー予想とは
『空間に球を詰め込む時、上記の方法が最も密度が大きくなるはずだ』
というもの
一見、当たり前のように思えるが、
これを数学的にちゃんと証明することは容易ではなかった
解決までになんと…
400年もかかった超難問！
証明の話をする前に
「平面充填」という考え方について解説していく
ここに無限に広がる平面があるとする
同じ図形をたくさん並べていく時、どんな図形だったら隙間なく覆いつくすことが出来るか？
図形は回転、反転してもOK
まずは三角形
三角形は平面を覆いつくせるか？
どんな三角形も回転させて、つなぎあわせると平行四辺形になる
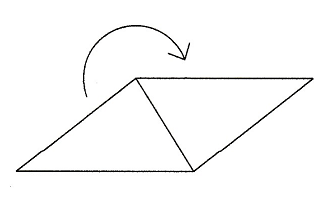
平行四辺形は横に無限に並べられるし、縦にも広げられる
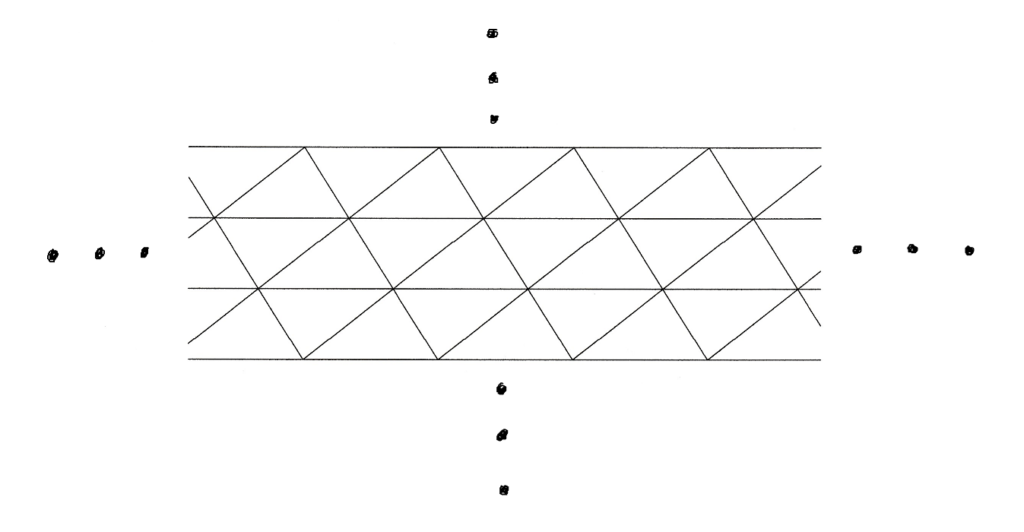
すると、平面を充填出来ることが分かる
この時、数学では
「三角形は平面充填可能」
という
次に四角形
どんな四角形も回転させて、つなぎあわせると…
六個の辺が互いに平行になる平行六辺形という形になる
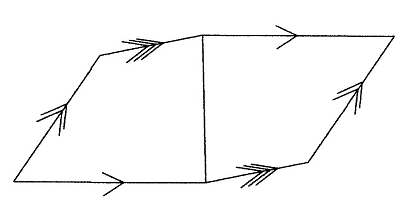
平行六辺形はこんな風に並べていくと、
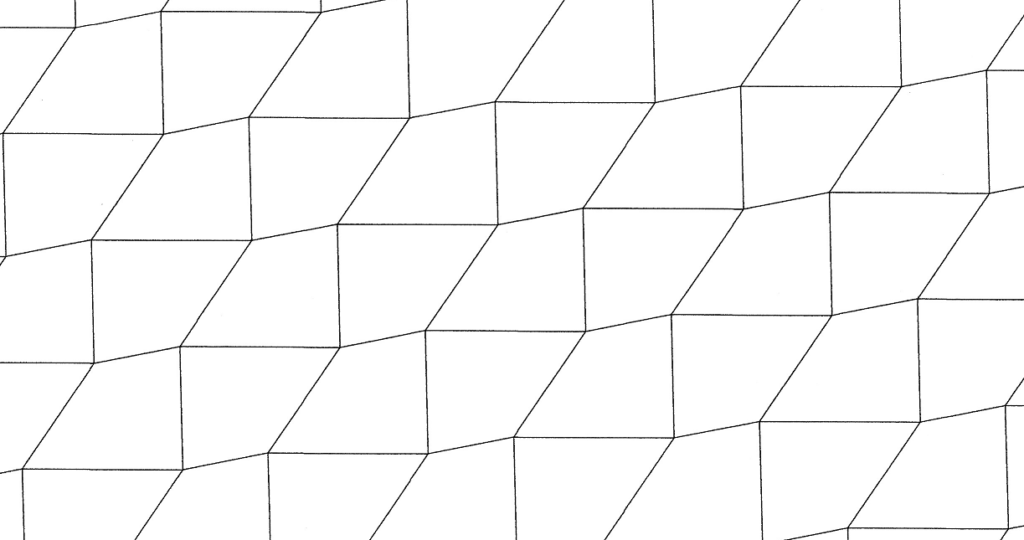
平面を覆いつくすことが出来るので、
「四角形は平面充填可能」
次は五角形を飛ばして
六角形について
平行六辺形についてはすでに四角形で平面充填可能
それ以外の六角形は平面充填出来ないケースがほとんどだった
平面充填可能な六角形は下記の3タイプ
タイプ1
（平行六辺形はここに含まれる）
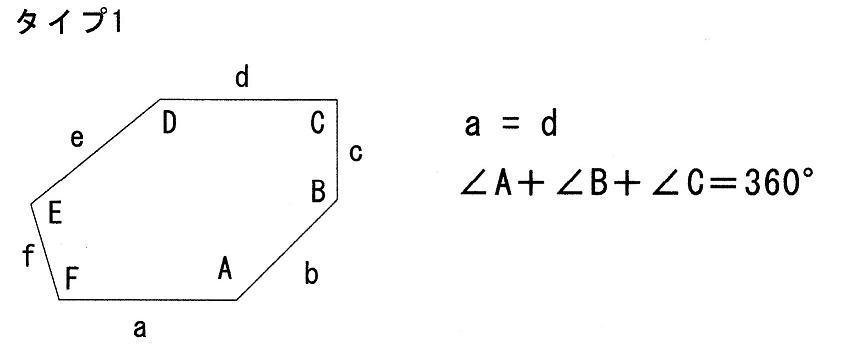
タイプ2
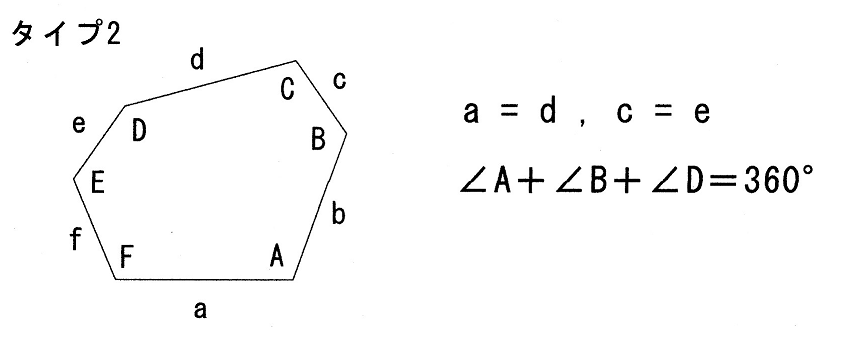
タイプ3
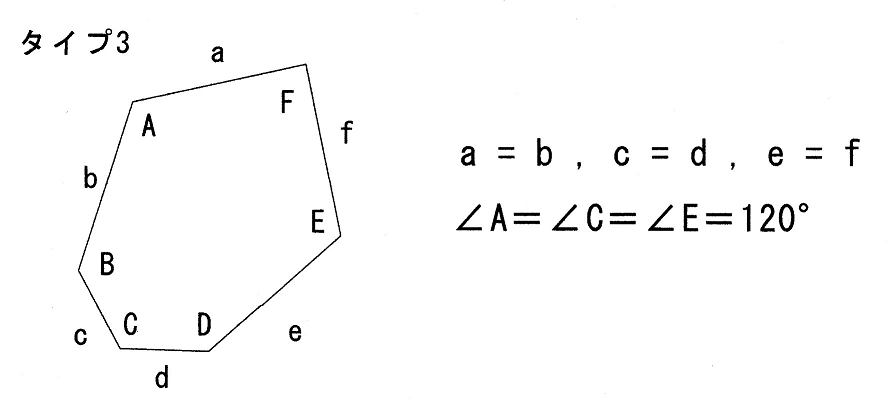
ちなみに七角形以上は平面充填不可能であることが証明されている
残るは五角形について
平面充填可能な五角形だけは最近まで未解決問題だった（2023年時点）
古くから知られていたのは5つのタイプ
ドイツの数学者
カール・オーガスト・ラインハルト（1895ー1941）
1918年に発表
五角形の各頂点をA~E、各辺をa～eとするとき、
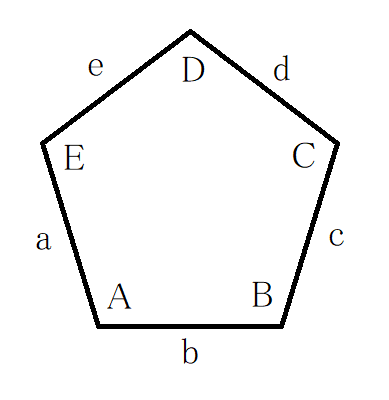
タイプ１
∠A＋∠B＋∠C＝360°
タイプ２
∠A＋∠B+∠D＝360°
a = d
タイプ３
∠A＝∠C＝∠D＝120°
a = b , d = c ＋ e
タイプ４
∠C＝∠E＝90°
a = e , c = d
タイプ５
∠A＝120° , ∠C＝60°
a = b , c = d
それ以降、新しいタイプは全然見つからなかった
ところが半世紀後の1968年
アメリカの数学者
リチャード・ブランドン・カーシュナー（1913−1982）
新たに3つのタイプを発見
タイプ6
∠A＋∠B＋∠D＝360°
∠A＝2∠C
a = b = e , c = d
タイプ７
2∠B＋∠C＝360°
2∠D＋∠A＝360°
a = b = c = d
タイプ8
2∠A＋∠B＝360°
2∠D＋∠C＝360°
a = b = c = d
1975年
リチャード・ジェームズⅢ
タイプ10を発見
タイプ10
∠A＝90° , ∠B＋∠E＝180°
2∠D＋∠E＝360° , 2∠C＋∠B＝360°
a = b = c ＋ e
1976年ー1977年
数学とはほとんど縁のない普通の主婦
マジョリー・ライス
タイプ9、タイプ11、12、13を発見
タイプ9
2∠E＋∠B＝360°
2∠D＋∠C=360°
a = b = c = d
タイプ11
∠A＝90° , ∠C＋∠E＝180°
2∠B＋∠C=360°
d = e = 2a ＋ c
タイプ12
∠A＝90° , ∠C＋∠E＝180°
2∠B＋∠C=360°
2a = d = c ＋ e
タイプ13
∠A＝∠C＝90° , 2∠B＋∠D＝360°
∠B＝∠E
2c = 2d = e
1985年
ドイツの数学者
ロルフ・シュタイン
タイプ14を発見
タイプ14
∠A＝90° , ∠C＋∠E＝180°
2∠B＋∠C＝360°
2a = 2c = d = e
2015年
スーパーコンピューターを使用して
ケイシー・マン
ジェニファー・マクラウド・マン
デビッド・ヴァン＝デラウ
らがタイプ15を発見
タイプ15
∠A＝90° , ∠B＝150° , ∠C＝60°
2a = 2b = 2d = c
2017年
マイケル・ラオ
「平面充填可能な五角形は15タイプで打ち止めである」
という論文を発表
さてケプラー予想は
球についての問題なので平面では円で考えてみる
『平面に円を敷き詰めるとき、円の密度が最も大きくなる方法は？』
最初でもやったように規則正しく並べた方が密度が大きいはずである
この「円充填問題」という当たり前のように思える問題だが、
数学的にきっちり証明できたのは1940年代だった
なぜなら
無限に続く平面に円を敷き詰めるとき
規則正しく並べるよりも、もしかしたらランダムに敷き詰めた方が効率が良いかもしれない
例えば
規則正しく並べた場合、周りに6つしかない
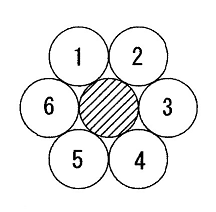
ランダムに並べた場合、周りに7つあることもある
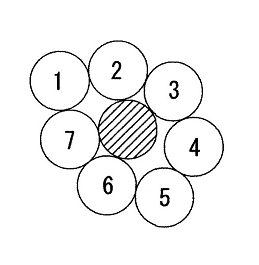
実はこの問題は真剣に考え出すととても難しい
ここで登場するのが
カール・フリードリヒ・ガウス（1777−1855）
ケプラー予想を詳しく研究していた
まずは規則的な並べ方に限定して研究し、
円の密度（平面に占める円の割合）は、およそ90.69％だということが分かった
（ラグランジュの研究と合わせて事実上規則的配置の場合を証明したとされる）
しかし、ランダムな並べ方についても、これが最大なのかについての研究は残さなかった
円充填の問題を解決したのは
ハンガリーの数学者
ラスロ・フェイエシュ＝トート（1915ー2005）
幾何学の論文を180本以上発表するなど、充填問題の権威として知られている
1940年に発表した論文
「ある幾何学の定理について」
それまで誰も辿り着けなかったランダムな並べ方を含む円充填問題の証明だった
まずは有限の広さの領域に円を並べていくというもの
面積Tにランダムで半径r の円をn個敷き詰める
円1個の面積 ＝ πr2
なので、
n個の円の面積の合計 ＝ nπr2
ということは円の密度は
で表される
では、n個の円の面積の合計が最も大きくなるのはどんな場合か？
そこでn個の円の面積の合計を調べるために
“円と円の真ん中に線を引き、n個の多角形を作っていく“
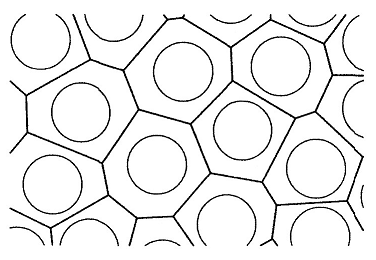
n個の多角形には様々な多角形があるが、
どの多角形の面積も（規則正しく敷き詰めた場合に出来る）正六角形の面積よりも大きいことを突き止めた
正六角形の面積 ≦ 多角形の面積
正六角形の面積は2√3r2
ということは
n個の合計の面積であっても
n ×2√3r2 ≦ n個の多角形の面積の合計
になる
これを変形して
先ほどの円の密度の式に、この不等式を代入すると
ここで（n個の多角形の面積の合計）／Tに着目すると
領域Tが無限に大きくなるとn個の多角形の面積の合計は領域Tと一致するので
（n個の多角形の面積の合計）／T ＝ 1
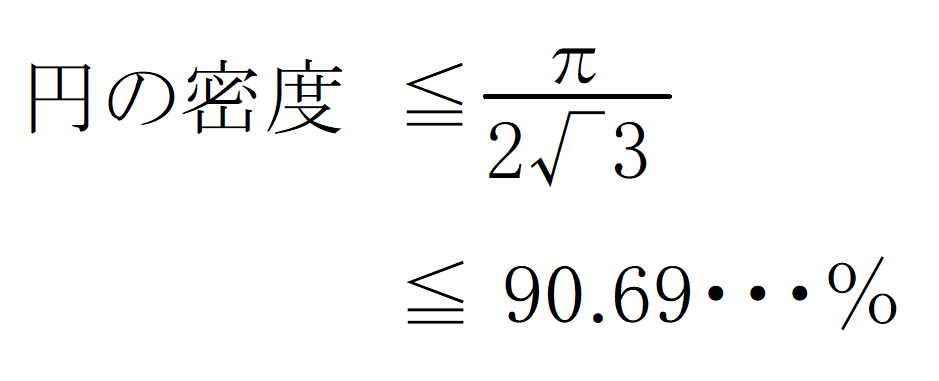
となる
よって、円の密度は90.69％以下ということになり、
最大は90.69％であることが証明された
これはガウスが考えた「規則的な並べ方の密度」と同じ
つまり、ランダムな並べ方を含めてもこれが最大である！
とここまで平面における円充填の問題を考えてきたが、
ここからやっと3次元における球の充填問題（ケプラー予想）に入る
もう一度確認しておこう
ケプラー予想とは
『空間に球を詰め込む時、規則正しく敷き詰める方法が最も密度が大きくなるはずだ』
16世紀
ドイツの小さな町で生まれた
ヨハネス・ケプラーは
聖職者も志したこともあり
『神は完全なる世界を創造されたので
宇宙は幾何学的原理に支配されているはずだ』
と考えていた
40歳頃、友人に自分の本を送った
その本の中に
「稠密六方格子と面心立方格子の混合が球の密度が最大になる」
と書き記されていた
しかし、この予想についての証明は書かれていなかった
この『球充填問題』に対し一つの結論を出したのが…
またしても
カール・フリードリヒ・ガウス（1777−1855）
ここでも規則的な並べ方に限定して研究し、
球のくぼみに置いていく並べ方が一番密度が高いことを事実上証明した（とされる）
その密度（空間に占める球の割合）はおよそ74.05％
しかし、円充填問題のときと同様に
ランダムな並べ方を含めてもこれが最大なのかまでは調べなかった
1900年
ドイツの数学者
ダフィット・ヒルベルト（1862−1943）
20世紀中に解かれるべき23の未解決問題を発表
その中に「ケプラー予想」が含まれた
ここで「ケプラー予想」の解決に名乗りを上げたのが
ラスロ・フェイエシュ＝トート（1915ー2005）
円充填問題を解決した時のように、
球と球の真ん中を面で区切って多面体を作ってみた
ここで使用した多面体は正十二面体
n個の正十二面体の体積 ≦ n個の多面体の体積
ということが計算できれば最大の密度を導ける
ところがこのアプローチには欠陥があり、証明には辿り着けなかった
理由は
そもそも正十二面体では空間を隙間なく充填することが不可能だったのである
20世紀の終わり
結末は思いもよらぬ方法だった・・・
1998年
アメリカの数学者
トマス・ヘールズ
最先端のコンピュータと科学計算用ソフトウェアを駆使し、
膨大な場合分けをしらみ潰しに調べ尽くし、
ようやくランダムな並べ方を含めても最大の密度は74.05％である
ことが証明された
が、コンピュータを使用した証明は当初なかなか受け入れられなかった
ヘールズはその後も11年にも渡る研究を積み重ね、現在では誰もが認めるようになっていった
まさかケプラー予想の結末がコンピュータを使用した証明になると一体誰が想像できただろうか
これでやっとケプラー予想が解決したにも関わらず、数学者たちはこれで満足はしなかった
そう数学は2次元、3次元ときたら…
次は高次元空間の充填問題に取り組みたくなるもの
2022年
数学界に一つのニュースが流れた
ウクライナの数学者
マリナ・ヴィヤゾフスカ（スイスにある大学）
8次元と24次元の球充填問題を解決した
これによって2022年のフィールズ賞を受賞
数学者たちが高次元の球充填問題に興味を持ち始めたきっかけは、
10次元での意外な発見だった
高次元でも最も密度が大きくなるのは、やはり規則的な並べ方ではないかと考えられていた
しかし、10次元の空間では既知の格子充填よりも密度が大きい非格子充填の存在が分かった
数学は次から次へと困難の連続だ
ウクライナの数学者
マリナ・ヴィヤゾフスカはこう言う
「この世界に人々の心を一つに出来るものが少なくなっています。
数学はその数少ない一つ（人々の心を一つに出来るもの）だと思っています。
どうかアイデアの共有を止めず、
お互いが心を開いて数学に関する問題はもちろん
一緒にこの時代の困難に対する答えを見つけてくれることを願っています。」
（終わり）
最後まで読んで頂き、誠にありがとうございます。
またいつでもいらしてください。
その他のお話
笑わない数学（シーズン２）「1+2+3+4+…＝－1/12（無限級数）」のまとめ
笑わない数学（シーズン２）「ケプラー予想」のまとめ
笑わない数学（シーズン２）「超越数」のまとめ
笑わない数学（シーズン２）「結び目理論」のまとめ
笑わない数学（シーズン２）「1＋1＝2」が正しい理由のまとめ
笑わない数学（シーズン2）「コラッツ予想」のまとめ
笑わない数学（シーズン2）「非ユークリッド幾何学」のまとめ
