MENU
テレビ番組

笑わない数学（シーズン２）「超越数」のまとめ

kikorikori
記事内に商品プロモーションを含む場合があります

今回のテーマは「超越数」
人智を超えたウルトラスーパーな数
超越数とは一体どんな数なのか

およそ2400年前・・・

古代ギリシャの数学者
アナクサゴラス（紀元前500ごろー紀元前428ごろ）
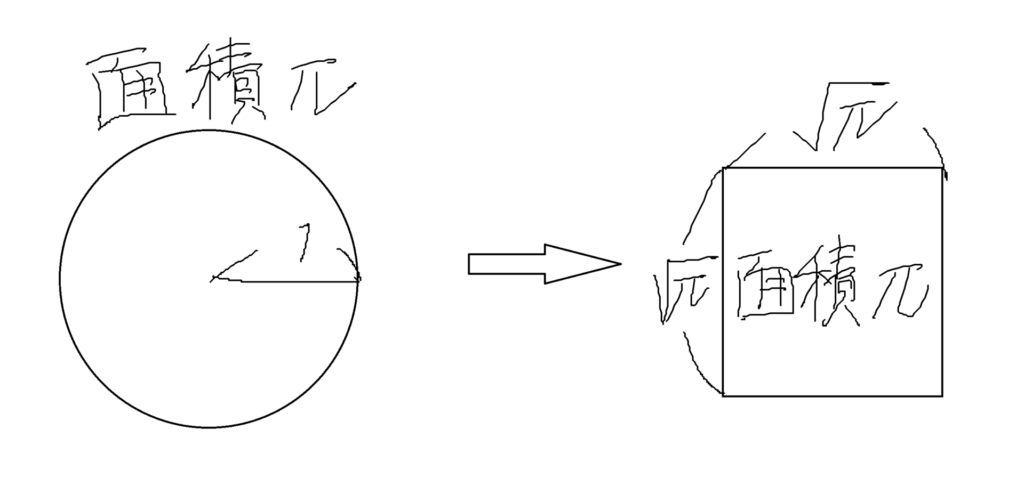
半径1の円と同じ面積の正方形は描けるか？
（使用しても良いのは、定規とコンパスのみ）

この問題はつまり
長さ√πの正方形が描けるのか、ということ

その前に、
まずは長さ1から3の長さが描けるかどうかを確かめてみよう

定規で直線を描いて、コンパスで3回円弧を作図する

では、長さ1/3はどう描くか

適当に描いた直線に直線上の任意の点を中心としてコンパスで長さ1の円弧を二つ作る

（直線に対して垂線を描く作図、垂直二等分線）
次に二つの円弧と直線の交点から適当な長さの円弧を描く
この円弧の交点と直線上にとった円弧の中心とを線で結ぶ

続いて、この線に3の長さの線をコンパスで作る

長さ3の点と最初に描いた直線と円弧の交点を結び、直角三角形を作る

長さ2の点から垂線を描くと、このようになった

すると小さな直角三角形（赤い部分）と大きな直角三角形は相似（※）であることが分かる

ということは、赤い線の部分は

底辺の比＝高さの比
1：3＝赤い線：1
赤い線＝1／3

1／3ということが分かった

ここまで作図してきたことを応用すれば、
5の長さも、1／5の長さも、3／5の長さも作図することが出来る
つまり、『どんな自然数の長さも、どんな分数（有理数）の長さも描ける』ということ

ルート（無理数）も作図することが出来る

長さ1と任意の長さaがあり、直線に 1＋a の長さを作る

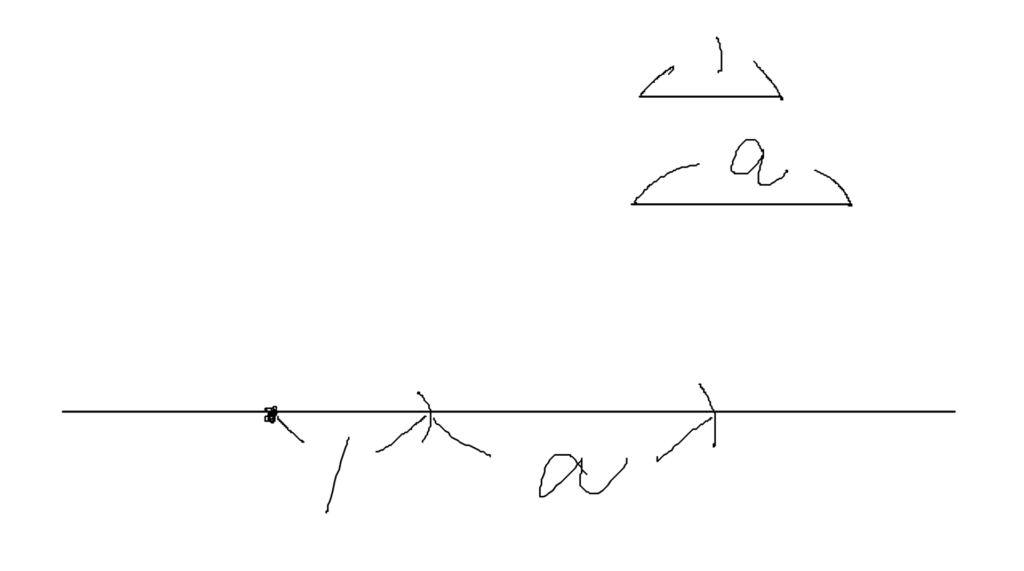
（中点の作図、垂直二等分線）
それぞれの端点から適当な長さのコンパスを両側に描いて、それぞれの交点を線で結ぶ

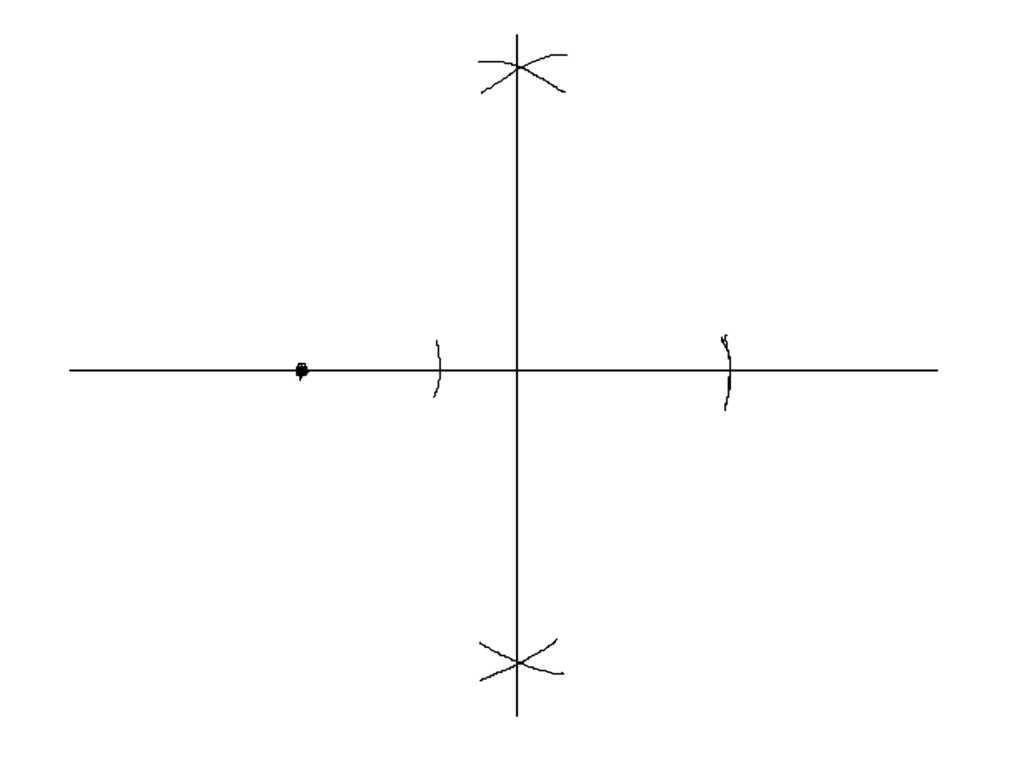
すると、この線と　”長さ1＋a” の交点が　”長さ1＋a” の中点となる
この中点を中心とした ”半径（1＋a）／2” の半円を描いて、長さ1の点から垂線を描く

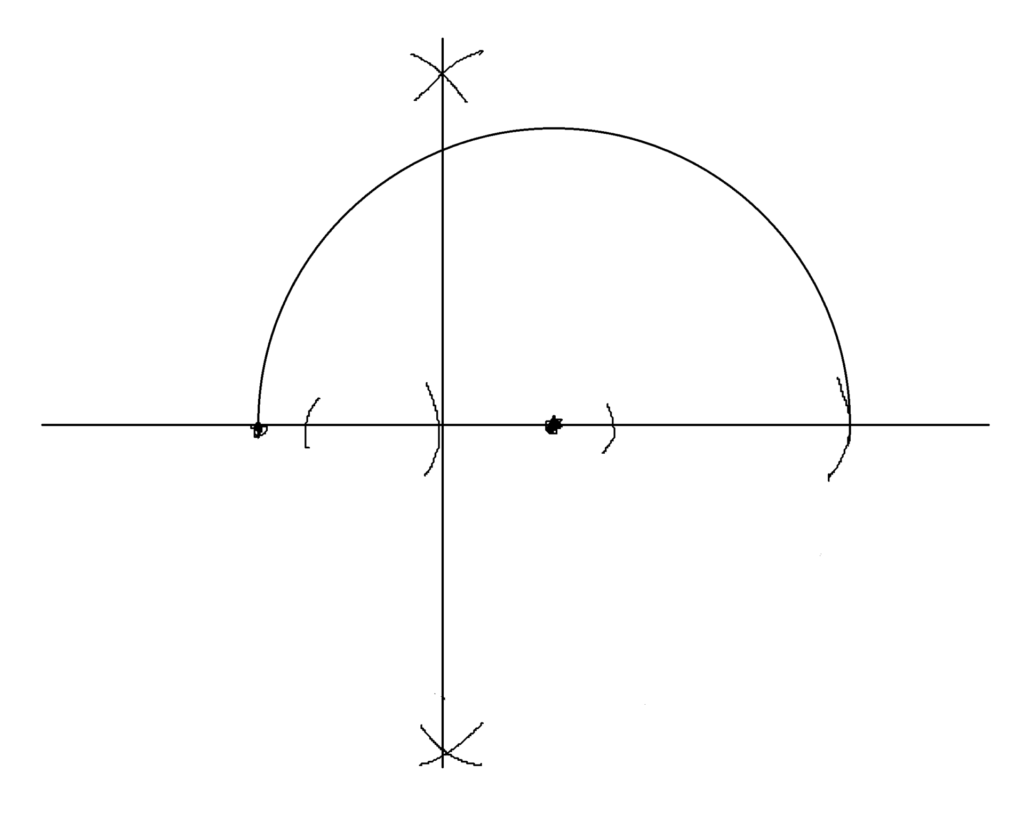
円と垂線の交点と長さ 1＋a の端点をそれぞれ結ぶと、二つの相似な三角形が出来る
（二つの三角形が相似であることの証明はこちら1）

赤い線の部分をXとして比の計算をすると

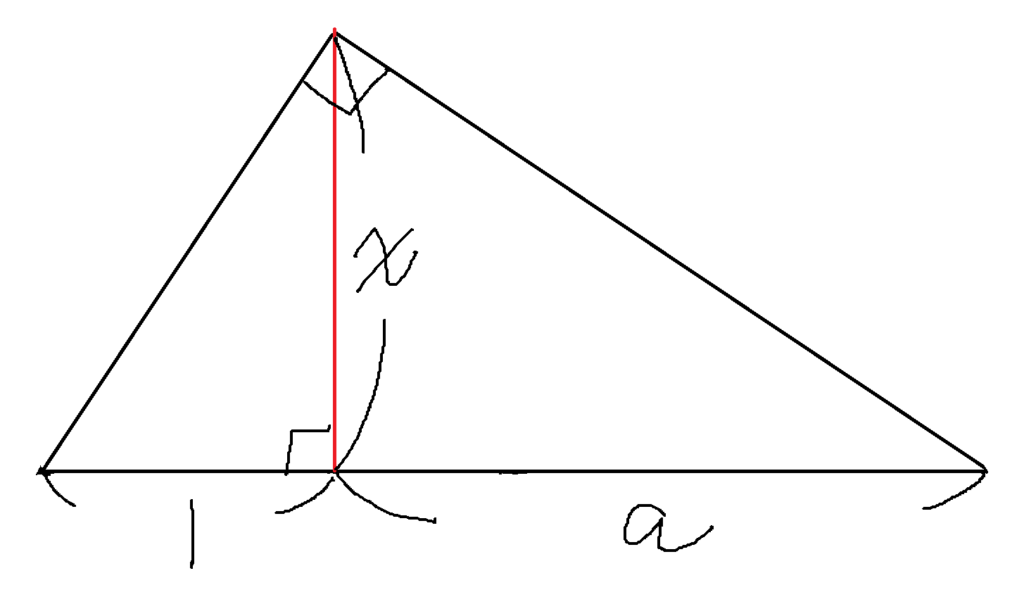
1：X＝X：a
X2＝a
X＝√a

これで作図出来る長さであれば、ルート（無理数）も作図出来ることが分かった

しかし、アナクサゴラスはどう作図してもπを作図する方法が見つからなかった

なぜπは作図できないのか？

その理由を全く新しいアプローチで解き明かせないかと考えたのが
19世紀のドイツの数学者で「πの征服者」との異名をもつ
フェルディナント・フォン・リンデマン（1852ー1939）
自然数、分数（有理数）、無理数（作図出来る長さ）にはそれぞれに対応する方程式が存在する

例えば、
1／3は、3Xー1＝0という方程式の解（答え）
√2は、X2ー2＝0という方程式の解

実は作図出来るものは何かしらの方程式の解になっている

方程式の解になるものを「代数的数」とすると、
作図できる数は代数的数に含まれている

ということは、代数的数でなければそもそも作図することは出来ない

そして、この代数的数に含まれない数を「超越数」とした

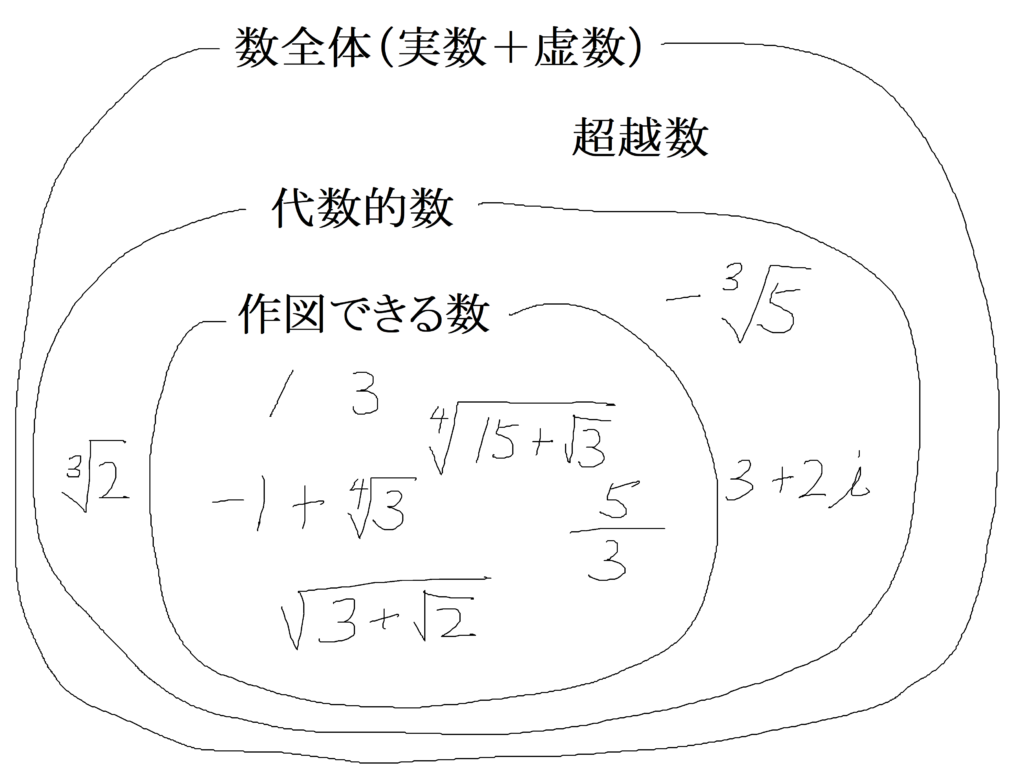
つまりπが超越数であることが証明できれば、作図できないことが証明される

思い返してみると、
中世までの数学は古代ギリシャの時代から代数的数については徹底的に調べられてきた
フェラーリ、カルダーノ、ガロアらの高次方程式の解に関する研究など…
数学者たちが今まで扱ってきたのは全て代数的数だった…と言っても過言ではない
（ちなみに虚数も代数的数）

人智を超えた超越数とは一体どんな数なのか

リンデマン以前の数学者たちの超越数探しはどうだったのか

18世紀
もしかしたら超越数なんじゃないか疑われていたのが、πとe（自然対数の底）
（この頃はまだ「超越数」という言葉はなく、概念的なものだけ）

19世紀前半
ジョゼフ・リウヴィル（1809ー1882）
eが超越数であることを証明しようとしたがなかなか辿り着けなかった
もはや超越数の存在に対しても懐疑的になっていた
もう証明出来ないなら、人工的に超越数なるものを作ってしまおうと思いつく

そこで誕生したのが下にある「リウヴィル数」である

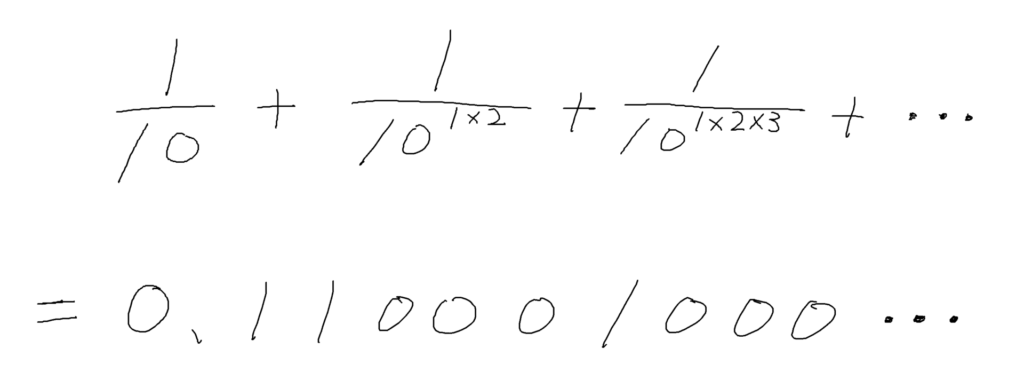
この数が超越数であることを証明した

1873年
シャルル・エルミート（1822ー1901）
eが超越数であることを背理法を使って証明

eが超越数ではなく、代数的数であると仮定する
すると下式が成り立つ

an・en ＋ an−1・en−1 ＋ … ＋ a0 ＝0
（an、…、a0は整数）

ここからある奇妙な数Jが求まる
このJは
「ものすごーーーく大きい数でもあり、かなり小さい数でもある」
という矛盾が生じてしまう

つまり、仮定が間違っているのでeが代数的数というのは誤り

よって、eは超越数である！！！

1882年
πが超越数であることを証明したのが、
「πの征服者」との異名をもつフェルディナント・フォン・リンデマン

エルミート・リンデマンの定理
「αが代数的数ならばeαは超越数である（ただし、α≠0）」
を発見

【πが超越数であることの証明】
”πは代数的数である”と仮定する
虚数iは代数的数なので、i × πも代数的数になる
エルミート・リンデマンの定理より
iπが代数的数ならばeiπは超越数である
ところが、
オイラーの式「eiπ ＝ −1（代数的数）」
と矛盾するので仮定が誤り

つまり、πは超越数である（終）

その後も超越数探しは白熱していくがなかなか見つからない

ゲオルク・カントール（1845ー1918）
自然数の個数∞ ＜ 実数の個数∞
実数の個数の方が圧倒的に多いことをすでに証明している

そこから自然数の個数は代数的数の個数と同じであることを証明

ということは、数全体の中で代数的数はほんの少ししかなく、大半は超越数である

イギリスのある数学者
「代数的数は漆黒の空にある星のように光っている。漆黒の闇は超越数である。」

超越数はまだまだ分からないことだらけ…

数学者たちの興味は「超越数の分類」に移っていく

2001年
マキシム・コンツェビッチ（1964ー　、フランス高等科学研究所　教授）
超越数の分類方法を提唱
「超越数が積分記号∫を使って表せるかどうか」

積分記号∫で表せる数を「周期」と定義した

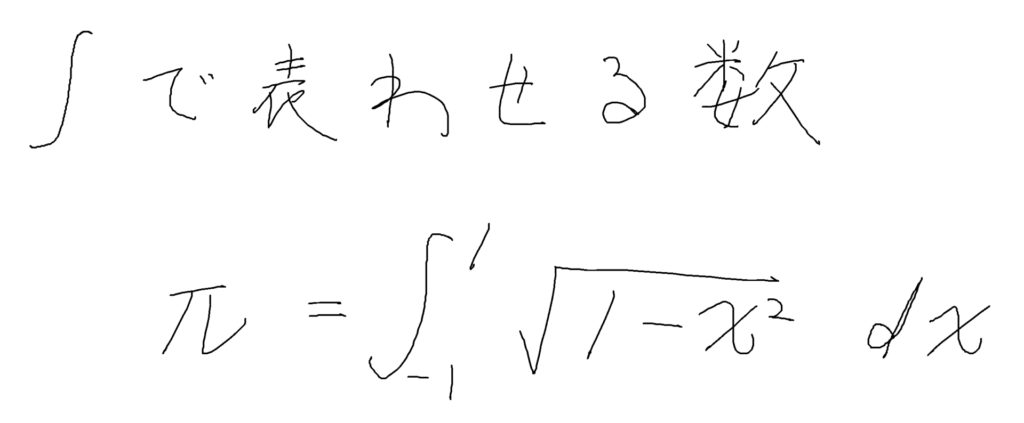
これによって超越数の中に周期が含まれることを証明した

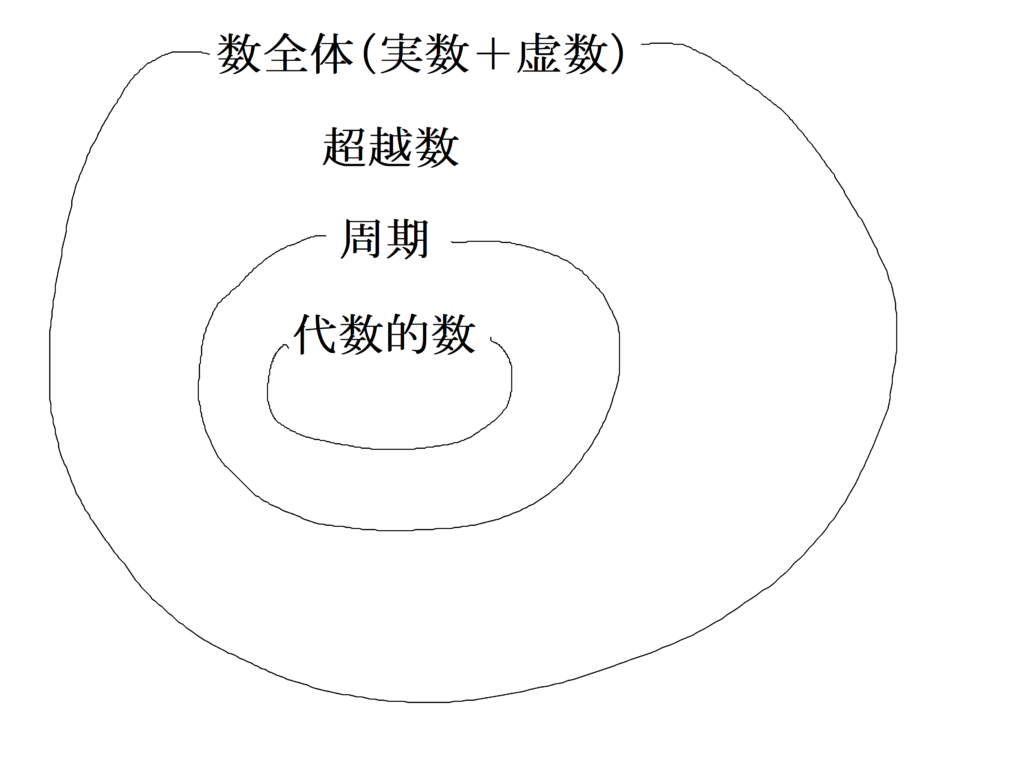
これは単なる仕分けにしか思えないかもしれない

しかし、超越数の分類は今後の数学を大きく進歩させると言われている

吉永正彦（大阪大学）　
「周期の登場は、今後長い期間人間の精神活動に喜びと活力を与え続け、
　数学を進展させるエネルギーを与え続けるのではないか」

「数」という広大な未知の世界で人類はようやく第一歩を踏み出したに過ぎない

（終わり）

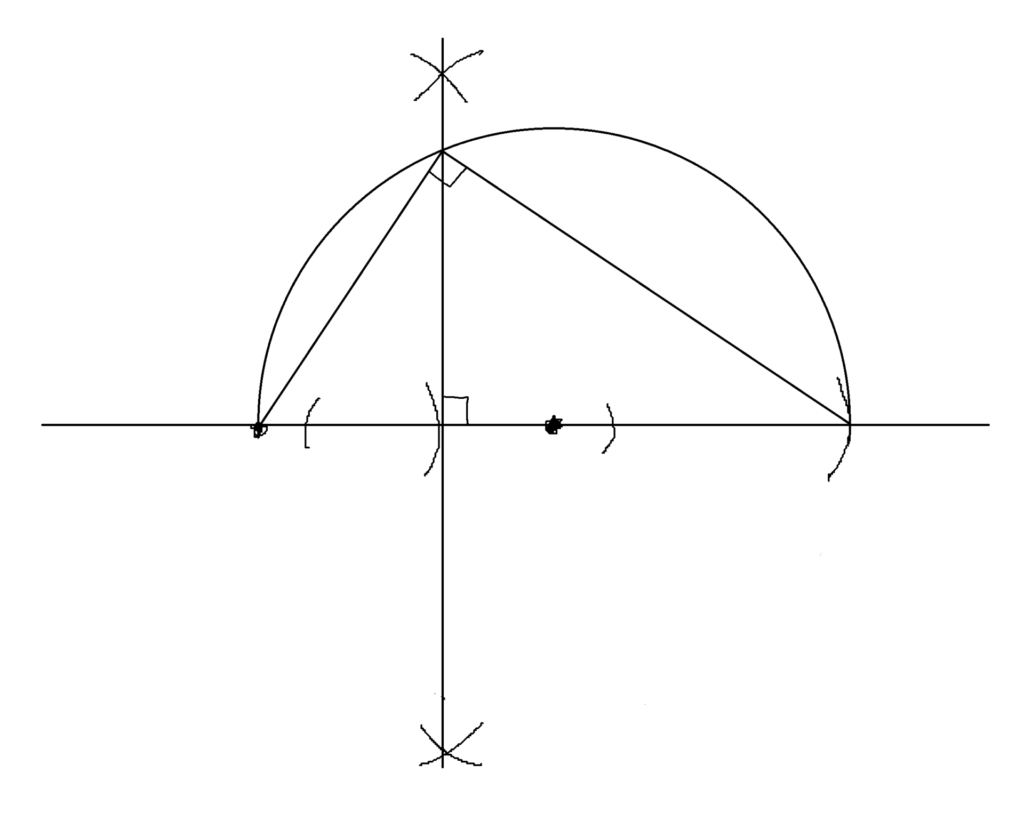
※相似・・・形（角度）は同じだけど、大きさ（長さ）が異なるもの

  1. ※相似の証明　　（続きに戻る） ↩︎

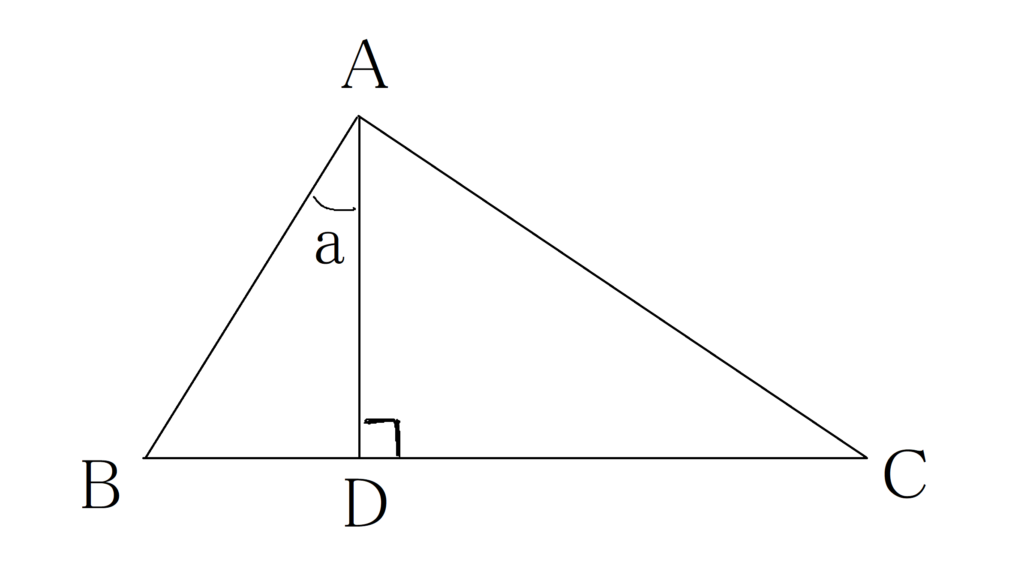
「半円に内接する三角形は直角三角形である」なので、
（タレスの「幾何学の五定理」より）

∠BAC＝90°
∠CAD＝90°－∠a　・・・①

△ABDにおいて
　∠ABD＝180°－（90°+∠a）
　∠ABD＝90°－∠a
①より
　∠ABD＝∠CAD

△ＡＢＤと△ＣＡＤは
　∠ＡＤＢ＝∠ＣＡＤ＝90°
　∠ＡＢＤ＝∠ＣＡＤ
よって、「２組の角がそれぞれ等しい」ので（相似条件）
　△ＡＢＤ∽△ＣＡＤ
（証明終了）

最後まで読んで頂き、誠にありがとうございます。
またいつでもいらしてください。

その他のお話

Recommend
こちらの記事もどうぞ
Translate »
記事URLをコピーしました