MENU
テレビ番組

笑わない数学（シーズン２）「結び目理論」のまとめ

kikorikori
記事内に商品プロモーションを含む場合があります

今回のテーマは「結び目理論」

結び目というと
一般的にはこういう結び目（端っこあり）を思い浮かべる

しかし、数学者たちの結び目は
こういう結び目（端っこなし）のことを考える
（結び目ということは「ヒモがほどけることはない」ということ）

では、ここで次の二つの結び目は同じ結び目でしょうか？

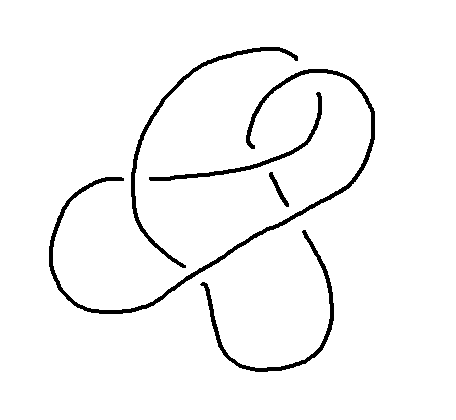
実は同じ結び目ということが分かる

結び目理論とは
「結び目が同じものなのか、違うものなのかを見た目だけで判定する理論」のこと

では、結び目には一体どんな種類があるのか
まずは結び目の分類を始めた頃に遡る

1870年代
物理学者のウィリアム・トムソン（1824−1907）
「原子の正体は何かの結び目みたいなものではないか」

つまり、元素の違いは結び目の種類の違いなのではないかと思いつく

この理論に興味を持ったのがトムソンの友人で
数学者のピーター・テイト（1831ー1901）
ヒモとヒモが交差する交点の数に着目して
交点の数をたよりにしらみつぶしに調べていった

交点0個
結び目なし

交点1個
一筆書き出来なければいけないので
交点1個の結び目も存在しない

交点2個
105通りの組み合わせがある
分裂してしまうもの、同じものを除いていくと
交点2個の結び目も存在しない

交点3個
1万395通りの組み合わせがある
分裂してしまうもの、同じものを除いていく
すると
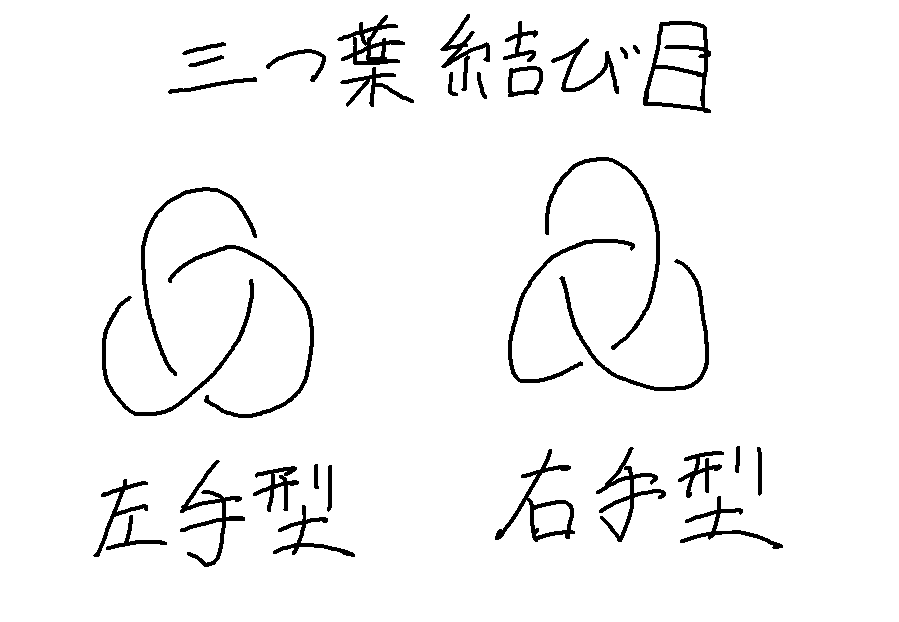
三つ葉結び目（左手型）と三つ葉結び目（右手型）の2種類を発見
この二つは鏡に写した関係

交点4個
202万7025通りの組み合わせがある

交点5個
6億5472万9075通りの組み合わせがある

交点6個
3162億3414万3225通りの組み合わせがある

交点7個
213兆4589億4667万6875通りの組み合わせがある

交点8個
の結び目を調べ始めましたが、
あまりの大変さに途中で挫折して止める

「これ以上結び目を分類する時間が見つけられない。
代わりに作業してくれる人物が大いに望まれる。」
という言葉を残した

その後

トーマス・カークマン（1806ー1895、イギリス）
1885年
交点10個までの結び目のリストを作成

と、ここまで分類はしてきたが、
根本的な問題としてどう変形しても違うものと言えるのか
結び目が同じなものなのか違うものなのか
数学的にきっちり判定しようという流れになり、
次の時代の数学者たちの大きな目標になっていた

そもそも結び目を見極めるのがなぜ難しいのか
それは結び目の形が自在に変化してしまうことにある
結び目はやろうと思うといくらでも複雑な形に変形できるので、
同じものかどうかを見極めるのはとても難しい

でも、もし変装しても変わらないものがあるとしたら…
例えば、人間で言うところの「指紋」のようなものがあれば分かるのではないか

そこで結び目の「指紋」探しが始まる

ジェームズ・アレクサンダー（1888ー1971）
アレクサンダー多項式の発見
ヒモが形作る交点Yとヒモが囲む領域Xから数式（文字式）に置き換えたもの
この多項式は変装しても変わらない「指紋」のような特徴がある

例えば
三つ葉結び（右手型）で
交点に番号
領域は交点につけた番号までをつける

交点と領域の表を作る

領域
123
交点①
②
③
領域Xは交点Yを…くぐる前の左側-t
くぐる前の右側1
くぐった後の左側t
くぐった後の右側-1
その他0

ヒモに向きをつける

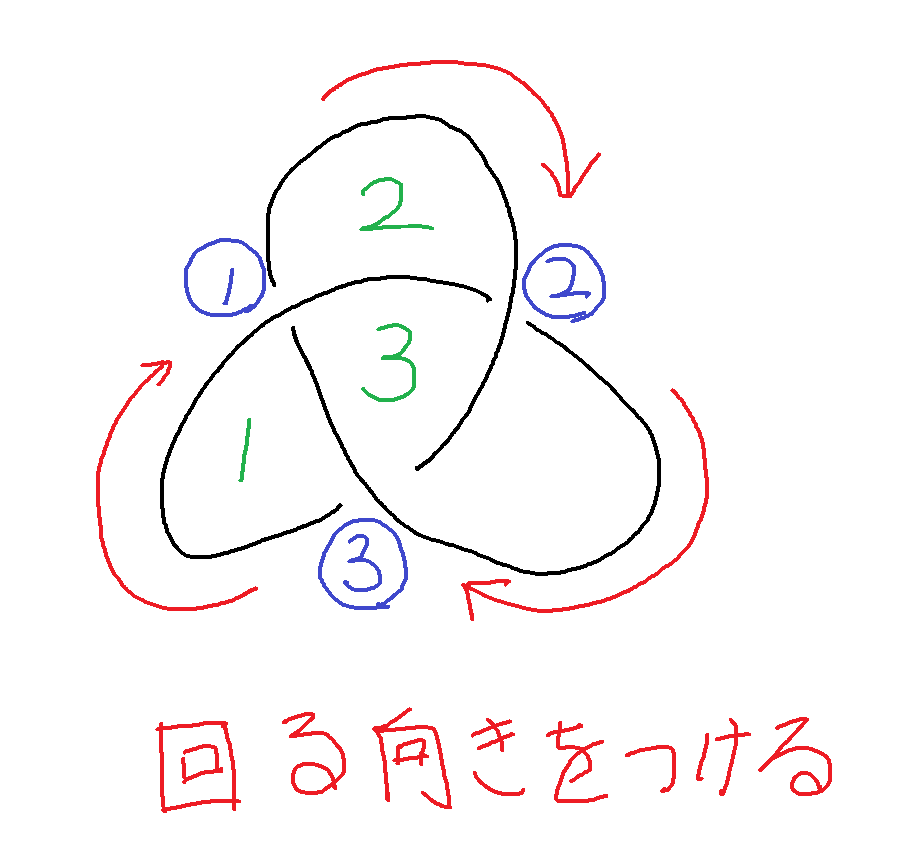
領域1は交点①をくぐる前の左側にあるので－t
領域2は交点①をくぐった後の右側にあるので−1
同様にして表を埋めていくと、

123
①-t-11
②0-t1
③-101

表を行列と見て行列式を計算する

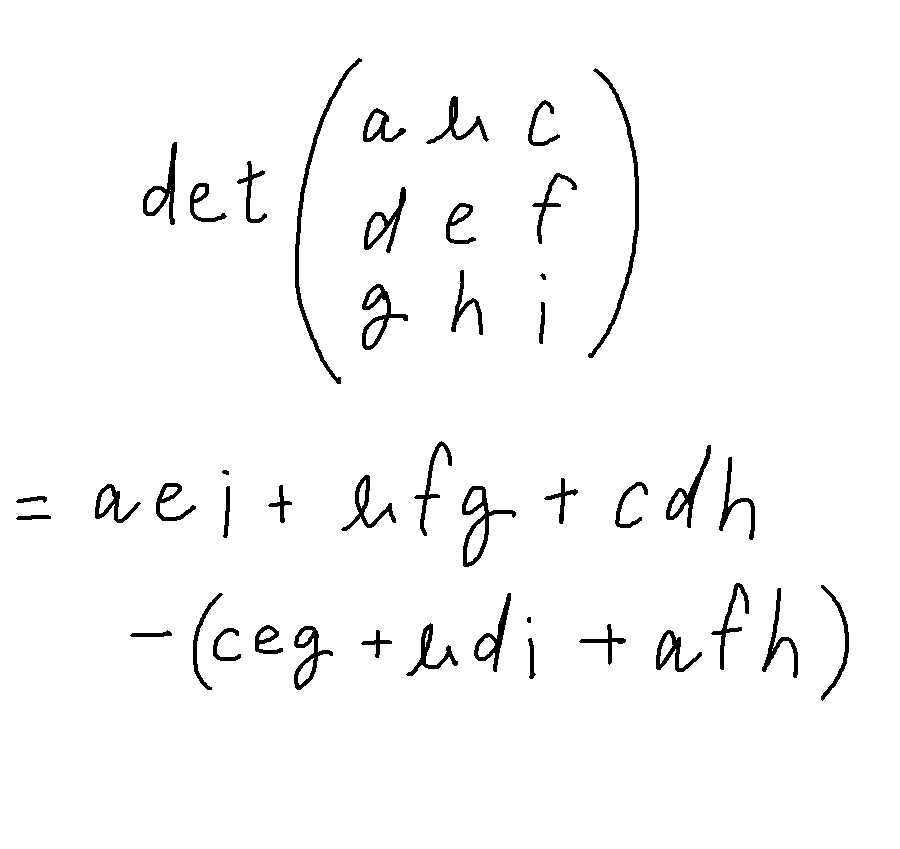
（a=-t , b=-1 , c=1 , d=0 , e=-t , f=1 , g=-1 , h=0 , i=1 を代入）

これに従っていくと
三つ葉結び（右手型）は　t2ーt＋1 となる
これがアレクサンダー多項式（指紋のようなもの）である

アレクサンダー多項式は本当に変装した結び目を見破ることが出来るのか
三つ葉結びを変形させた次の結び目はどうか

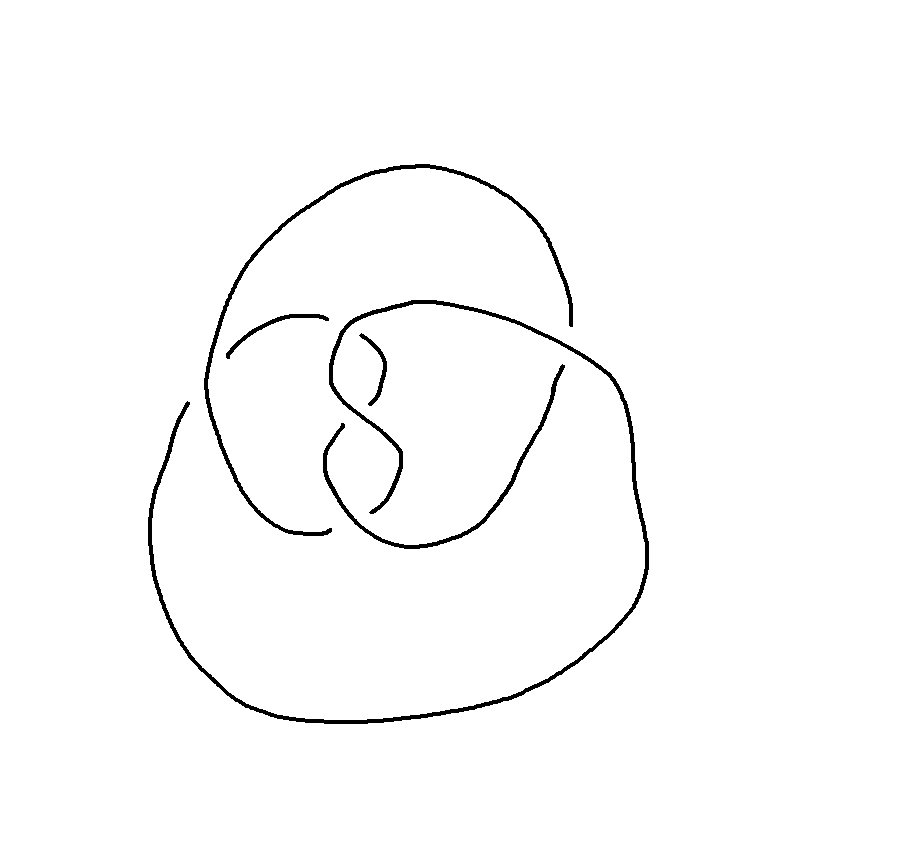
同じように交点と領域に番号を振って、
回る向きをつけて表を作る

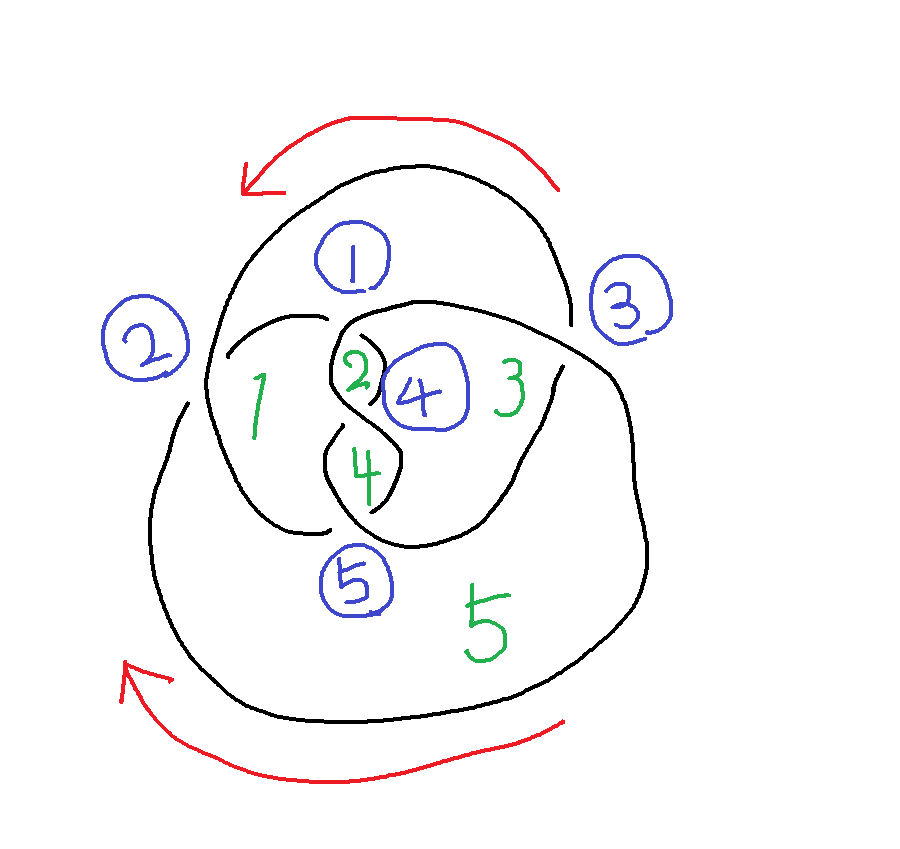
12345
①1-1t00
②-10001
③00-t01
④-11-tt0
⑤-t0-1t1

これを元に計算すると

t2ーt＋1

変装前の式と一致する
変装しても見つけることが出来た

しかし、
アレクサンダー多項式は万能ではなく、ある弱点があった
それは
三つ葉結び目（右手型）と三つ葉結び目（左手型）のような
鏡に写した関係の結び目を判別できないことにあった

それから半世紀が過ぎて、
新たな指紋（判別式）が発見されたのは

1984年
結び目理論とは全く関係のないところで発見された
ニュージランド出身の数学者
ヴォーン・ジョーンズ（1952ー2020、カルフォルニア大学バークレー校　教授）
ちょっとだけ聞きかじったことのある「結び目の数式」とそっくりな数式が
自分の専門分野に登場することに気づいた
そこから発展して誕生したのが「ジョーンズ多項式」である

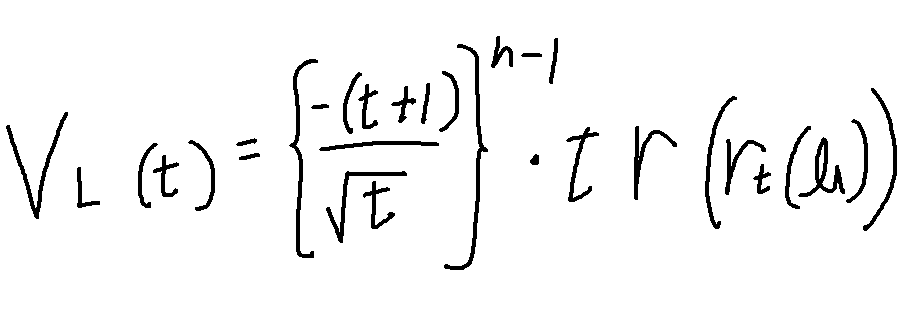
Lを表すn次ブレイドbをTemperley-Lieb代数への表現ｒtで送りトレースを取ってから補正した値

このジョーンズ多項式では鏡に写した三つ葉結び目を見分けることが出来た
これによって
1990年にフィールズ賞を受賞する

しかし、
ジョーンズ多項式も完璧ではなかった
交点9個までは判別出来たのだが、
交点10個以上になると判別出来なかった

指紋探しはまだまだ終わらず、
世界の数学者たちの心に火がついた

発表から数ヶ月後…

ジム・ホスティ
ケン・ミレット
レイ・リッコリッシュ
エイドリアン・オクネアヌ
ピーター・フレイド
デビッド・イェッター
ら6人の数学者が

さらに強力な指紋を発見

時を同じくして、ポーランドでも

ヨゼフ・プジティツキ
パヴェウ・トラチク
ら2人の数学者も発見

8人の数学者の頭文字をとってHOMFLYPT多項式（ホンフリーピーティー）と名付けられた

しかし、
これもまだ完全ではなかった

1993年
ロシア出身のフランス人数学者
マキシム・コンツェビッチ（1964ー　、フランス高等科学研究所　教授）
コンツェビッチ不変量を発見
ありとあらゆる結び目を判別できるのではないかと期待されている
現在、1番強力な指紋である

完璧な指紋を見つけるべく
数学者たちの探求はまだまだ続く…

とここまできて、
そもそも何で結び目なんか研究してるんだったっけ？

最初は原子を分類できるかも…から始まって、
次に数学者が勝手に興味をもって分類し始め、
次に結び目を見分ける数式を探し始めた
でもこれって
数学者が勝手に作り出したゲームのような単なる遊びに過ぎないのでは？

がしかし、
数学者たちが作り出した遊びのようなものが
宇宙を支配する自然法則を追い求める物理学の世界で不思議な事実が相次いで見つかった

20世紀末

フィールズ賞受賞者の理論物理学者
エドワード・ウィッテン（1951ー　、プリンストン高等研究所　教授）
自然法則に関する論文で
1989年「量子場の理論とジョーンズ多項式」を発表
ここでジョーンズ多項式を紹介

これは一体何を意味しているのか
実は数学者たちが勝手に作り出したはず結び目理論が、
人間とは関係のなく存在するはずの自然法則の中に宇宙誕生当初から組み込まれている可能性があるということ
（この「結び目理論」は物理学の世界で今も発展している分野「超弦理論（超ひも理論）」とは別物です）

人間が作り出した数学がなぜか宇宙と繋がってるというのは何とも不思議な話

そうなってくると
数学は人類が発明したものなのか、
それとも
人類が生まれる前から存在していて、それを人類が後から発見しただけなのか

皆さんはどう思うだろうか

思い返してみると、
あの非ユークリッド幾何学だって人間（数学者）が勝手に空想したものに過ぎない…
と思っていたら、
実はこの世界が非ユークリッド幾何学で出来ていたっていうこともあった

人類による発明だと思っていた数学が、
実は神様が大昔から使っていて、
人間はそれにようやく気づいただけなのかもしれない

そう思うと、
数学って一体何なのでしょう？

それではまた…

（終わり）

最後まで読んで頂き、誠にありがとうございます。
またいつでもいらしてください。

その他のお話

Recommend
こちらの記事もどうぞ
Translate »
記事URLをコピーしました